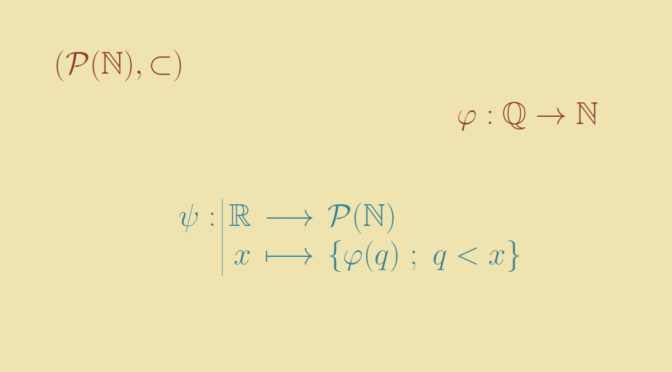Consider the set \(\mathcal P(\mathbb N)\) of the subsets of the natural integers \(\mathbb N\). \(\mathcal P(\mathbb N)\) is endowed with the strict order \(\subset\). Let’s have a look to the chains of \((\mathcal P(\mathbb N),\subset)\), i.e. to the totally ordered subsets \(S \subset \mathcal P(\mathbb N)\).

Some finite chains

It is easy to produce some finite chains like \(\{\{1\}, \{1,2\},\{1,2,3\}\}\) or one with a length of size \(n\) where \(n\) is any natural number like \[
\{\{1\}, \{1,2\}, \dots, \{1,2, \dots, n\}\}\] or \[
\{\{1\}, \{1,2^2\}, \dots, \{1,2^2, \dots, n^2\}\}\]

Some infinite countable chains

It’s not much complicated to produce some countable infinite chains like \[
\{\{1 \},\{1,2 \},\{1,2,3\},…,\mathbb{N}\}\] or \[
\{\{5 \},\{5,6 \},\{5,6,7\},…,\mathbb N \setminus \{1,2,3,4\} \}\]

Let’s go further and define a one-to-one map from the real interval \([0,1)\) into the set of countable chains of \((\mathcal P(\mathbb N),\subset)\). For \(x \in [0,1)\) let \(\displaystyle x = \sum_{i=1}^\infty x_i 2^{-i}\) be its binary representation. For \(n \in \mathbb N\) we define \(S_n(x) = \{k \in \mathbb N \ ; \ k \le n \text{ and } x_k = 1\}\). It is easy to verify that \(\left(S_n(x))_{n \in \mathbb N}\right)\) is a countable chain of \((\mathcal P(\mathbb N),\subset)\) and that \(\left(S_n(x))\right) \neq \left(S_n(x^\prime))\right)\) for \(x \neq x^\prime\).

What about defining an uncountable chain?

A chain having the cardinality of the continuum

Let’s first recall that the set of the rational numbers \(\mathbb Q\) is countable. Hence one can find a bijection \(\varphi : \mathbb Q \to \mathbb N\) (see following article).

Now consider the set of real numbers \(\mathbb R\) which has the cardinality of the continuum \(\mathfrak c = 2^{\aleph_0}\). For any real \(x \in \mathbb R\), we can define the set of rationals \(\psi(x) = \{q \in \mathbb Q \ ; \ q \lt x\}\). Then \(\varphi [\psi(x)]\) is a subset of \(\mathbb N\).

\(\left(\varphi [\psi(x)]\right)_{x \in \mathbb R}\) is a chain as for \(x \lt y\) we have \(\psi(x) \subset \psi(y)\). It has the cardinality of the continuum as \(\psi\) is one-to-one.