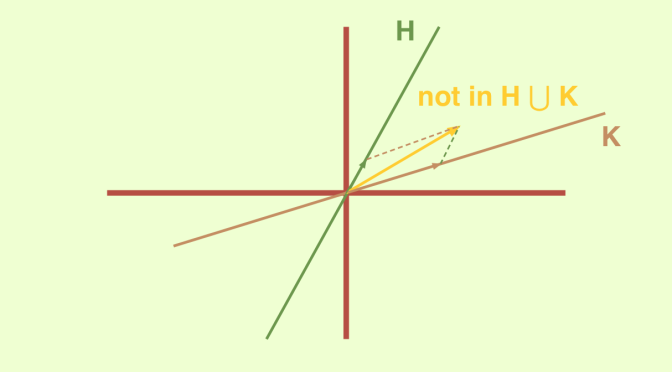
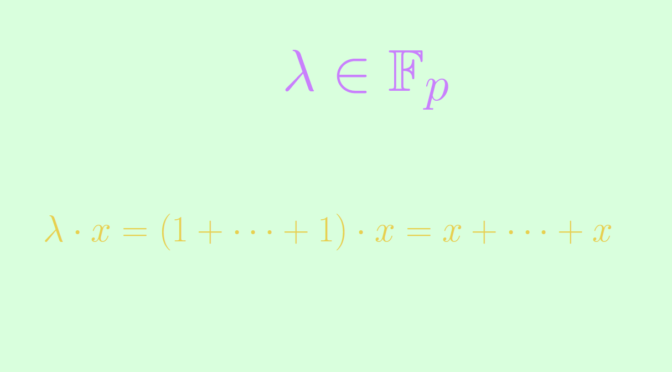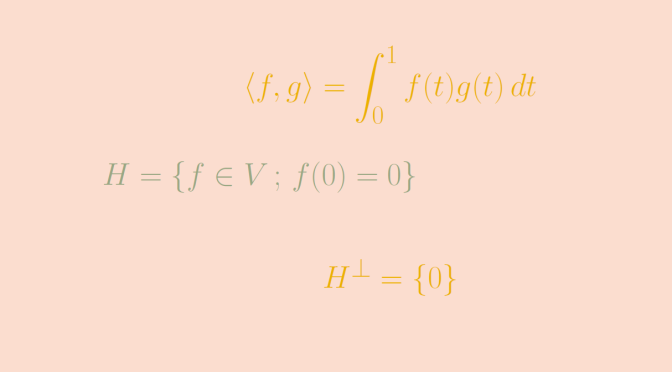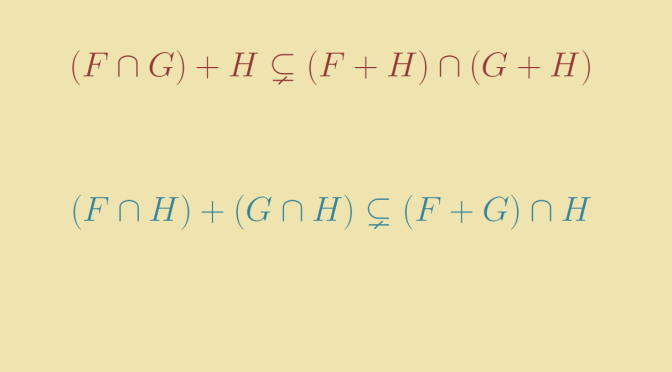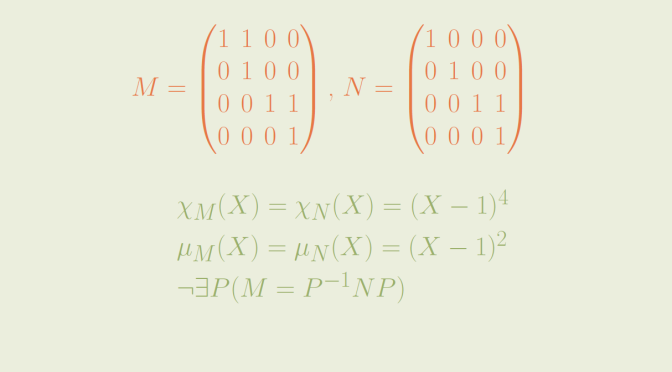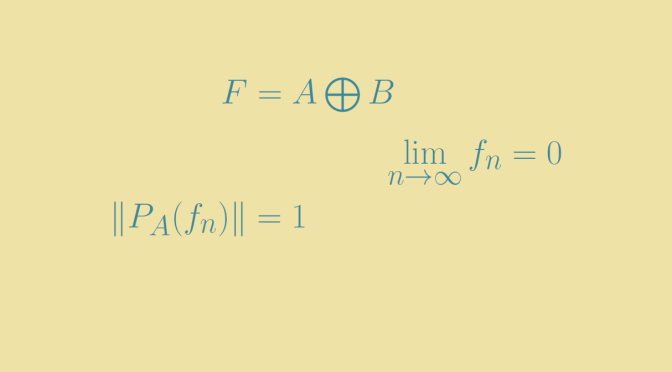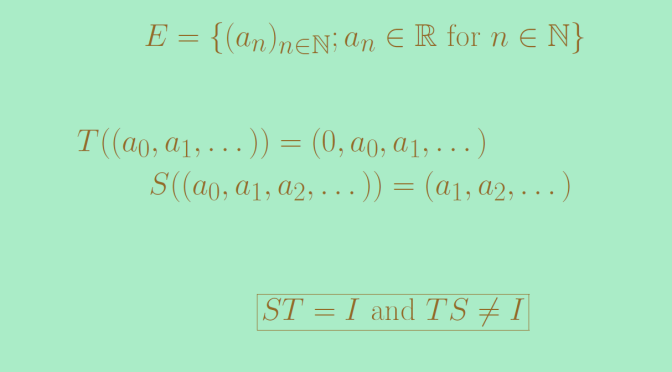Tag Archives: vector-spaces

Algebra

Additive subgroups of vector spaces

Leave a comment

Consider a vector space \(V\) over a field \(F\). A subspace \(W \subseteq V\) is an additive subgroup of \((V,+)\). The converse might not be true.

If the characteristic of the field is zero, then a subgroup \(W\) of \(V\) might not be an additive subgroup. For example \(\mathbb R\) is a vector space over \(\mathbb R\) itself. \(\mathbb Q\) is an additive subgroup of \(\mathbb R\). However \(\sqrt{2}= \sqrt{2}.1 \notin \mathbb Q\) proving that \(\mathbb Q\) is not a subspace of \(\mathbb R\).

Another example is \(\mathbb Q\) which is a vector space over itself. \(\mathbb Z\) is an additive subgroup of \(\mathbb Q\), which is not a subspace as \(\frac{1}{2} \notin \mathbb Z\).

Yet, an additive subgroup of a vector space over a prime field \(\mathbb F_p\) with \(p\) prime is a subspace. To prove it, consider an additive subgroup \(W\) of \((V,+)\) and \(x \in W\). For \(\lambda \in F\), we can write \(\lambda = \underbrace{1 + \dots + 1}_{\lambda \text{ times}}\). Consequently \[
\lambda \cdot x = (1 + \dots + 1) \cdot x= \underbrace{x + \dots + x}_{\lambda \text{ times}} \in W.\]

Finally an additive subgroup of a vector space over any finite field is not always a subspace. For a counterexample, take the non-prime finite field \(\mathbb F_{p^2}\) (also named \(\text{GF}(p^2)\)). \(\mathbb F_{p^2}\) is also a vector space over itself. The prime finite field \(\mathbb F_p \subset \mathbb F_{p^2}\) is an additive subgroup that is not a subspace of \(\mathbb F_{p^2}\).

Analysis

A discontinuous additive map

1 Comment

A function \(f\) defined on \(\mathbb R\) into \(\mathbb R\) is said to be additive if and only if for all \(x, y \in \mathbb R\)
\[f(x+y) = f(x) + f(y).\] If \(f\) is supposed to be continuous at zero, \(f\) must have the form \(f(x)=cx\) where \(c=f(1)\). This can be shown using following steps:

  • \(f(0) = 0\) as \(f(0) = f(0+0)= f(0)+f(0)\).
  • For \(q \in \mathbb N\) \(f(1)=f(q \cdot \frac{1}{q})=q f(\frac{1}{q})\). Hence \(f(\frac{1}{q}) = \frac{f(1)}{q}\). Then for \(p,q \in \mathbb N\), \(f(\frac{p}{q}) = p f(\frac{1}{q})= f(1) \frac{p}{q}\).
  • As \(f(-x) = -f(x)\) for all \(x \in\mathbb R\), we get that for all rational number \(\frac{p}{q} \in \mathbb Q\), \(f(\frac{p}{q})=f(1)\frac{p}{q}\).
  • The equality \(f(x+y) = f(x) + f(y)\) implies that \(f\) is continuous on \(\mathbb R\) if it is continuous at \(0\).
  • We can finally conclude to \(f(x)=cx\) for all real \(x \in \mathbb R\) as the rational numbers are dense in \(\mathbb R\).

We’ll use a Hamel basis to construct a discontinuous linear function. The set \(\mathbb R\) can be endowed with a vector space structure over \(\mathbb Q\) using the standard addition and the multiplication by a rational for the scalar multiplication.

Using the axiom of choice, one can find a (Hamel) basis \(\mathcal B = (b_i)_{i \in I}\) of \(\mathbb R\) over \(\mathbb Q\). That means that every real number \(x\) is a unique linear combination of elements of \(\mathcal B\): \[
x= q_1 b_{i_1} + \dots + q_n b_{i_n}\] with rational coefficients \(q_1, \dots, q_n\). The function \(f\) is then defined as \[
f(x) = q_1 + \dots + q_n.\] The linearity of \(f\) follows from its definition. \(f\) is not continuous as it only takes rational values which are not all equal. And one knows that the image of \(\mathbb R\) under a continuous map is an interval.

Algebra

A linear map without any minimal polynomial

Leave a comment

Given an endomorphism \(T\) on a finite-dimensional vector space \(V\) over a field \(\mathbb F\), the minimal polynomial \(\mu_T\) of \(T\) is well defined as the generator (unique up to units in \(\mathbb F\)) of the ideal:\[
I_T= \{p \in \mathbb F[t]\ ; \ p(T)=0\}.\]

For infinite-dimensional vector spaces, the minimal polynomial might not be defined. Let’s provide an example.

We take the real polynomials \(V = \mathbb R [t]\) as a real vector space and consider the derivative map \(D : P \mapsto P^\prime\). Let’s prove that \(D\) doesn’t have any minimal polynomial. By contradiction, suppose that \[
\mu_D(t) = a_0 + a_1 t + \dots + a_n t^n \text{ with } a_n \neq 0\] is the minimal polynomial of \(D\), which means that for all \(P \in \mathbb R[t]\) we have \[
a_0 + a_1 P^\prime + \dots + a_n P^{(n)} = 0.\] Taking for \(P\) the polynomial \(t^n\) we get \[
a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n = 0,\] which doesn’t make sense as \(n! a_n \neq 0\), hence \(a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n\) cannot be the zero polynomial.

We conclude that \(D\) doesn’t have any minimal polynomial.

Algebra

Non linear map preserving orthogonality

Leave a comment

Let \(V\) be a real vector space endowed with an inner product \(\langle \cdot, \cdot \rangle\).

It is known that a bijective map \( T : V \to V\) that preserves the inner product \(\langle \cdot, \cdot \rangle\) is linear.

That might not be the case if \(T\) is supposed to only preserve orthogonality. Let’s consider for \(V\) the real plane \(\mathbb R^2\) and the map \[
\begin{array}{l|rcll}
T : & \mathbb R^2 & \longrightarrow & \mathbb R^2 \\
& (x,y) & \longmapsto & (x,y) & \text{for } xy \neq 0\\
& (x,0) & \longmapsto & (0,x)\\
& (0,y) & \longmapsto & (y,0) \end{array}\]

The restriction of \(T\) to the plane less the x-axis and the y-axis is the identity and therefore is bijective on this set. Moreover \(T\) is a bijection from the x-axis onto the y-axis, and a bijection from the y-axis onto the x-axis. This proves that \(T\) is bijective on the real plane.

\(T\) preserves the orthogonality on the plane less x-axis and y-axis as it is the identity there. As \(T\) swaps the x-axis and the y-axis, it also preserves orthogonality of the coordinate axes. However, \(T\) is not linear as for non zero \(x \neq y\) we have: \[
\begin{cases}
T[(x,0) + (0,y)] = T[(x,y)] &= (x,y)\\
\text{while}\\
T[(x,0)] + T[(0,y)] = (0,x) + (y,0) &= (y,x)
\end{cases}\]

Algebra

A proper subspace without an orthogonal complement

Leave a comment

We consider an inner product space \(V\) over the field of real numbers \(\mathbb R\). The inner product is denoted by \(\langle \cdot , \cdot \rangle\).

When \(V\) is a finite dimensional space, every proper subspace \(F \subset V\) has an orthogonal complement \(F^\perp\) with \(V = F \oplus F^\perp\). This is no more true for infinite dimensional spaces and we present here an example.

Consider the space \(V=\mathcal C([0,1],\mathbb R)\) of the continuous real functions defined on the segment \([0,1]\). The bilinear map
\[\begin{array}{l|rcl}
\langle \cdot , \cdot \rangle : & V \times V & \longrightarrow & \mathbb R \\
& (f,g) & \longmapsto & \langle f , g \rangle = \displaystyle \int_0^1 f(t)g(t) \, dt \end{array}
\] is an inner product on \(V\).

Let’s consider the proper subspace \(H = \{f \in V \, ; \, f(0)=0\}\). \(H\) is an hyperplane of \(V\) as \(H\) is the kernel of the linear form \(\varphi : f \mapsto f(0)\) defined on \(V\). \(H\) is a proper subspace as \(\varphi\) is not always vanishing. Let’s prove that \(H^\perp = \{0\}\).

Take \(g \in H^\perp\). By definition of \(H^\perp\) we have \(\int_0^1 f(t) g(t) \, dt = 0\) for all \(f \in H\). In particular the function \(h : t \mapsto t g(t)\) belongs to \(H\). Hence
\[0 = \langle h , g \rangle = \displaystyle \int_0^1 t g(t)g(t) \, dt\] The map \(t \mapsto t g^2(t)\) is continuous, non-negative on \([0,1]\) and its integral on this segment vanishes. Hence \(t g^2(t)\) is always vanishing on \([0,1]\), and \(g\) is always vanishing on \((0,1]\). As \(g\) is continuous, we finally get that \(g = 0\).

\(H\) doesn’t have an orthogonal complement.

Moreover we have
\[(H^\perp)^\perp = \{0\}^\perp = V \neq H\]

Algebra

Intersection and sum of vector subspaces

Leave a comment

Let’s consider a vector space \(E\) over a field \(K\). We’ll look at relations involving basic set operations and sum of subspaces. We denote by \(F, G\) and \(H\) subspaces of \(E\).

The relation \((F \cap G) + H \subset (F+H) \cap (G + H)\)

This relation holds. The proof is quite simple. For any \(x \in (F \cap G) + H\) there exists \(y \in F \cap G\) and \(h \in H\) such that \(x=y+h\). As \(y \in F\), \(x \in F+H\) and by a similar argument \(x \in F+H\). Therefore \(x \in (F+H) \cap (G + H)\).

Is the inclusion \((F \cap G) + H \subset (F+H) \cap (G + H)\) always an equality? The answer is negative. Take for the space \(E\) the real 3 dimensional space \(\mathbb R^3\). And for the subspaces:

  • \(H\) the plane of equation \(z=0\),
  • \(F\) the line of equations \(y = 0, \, x=z\),
  • \(G\) the line of equations \(y = 0, \, x=-z\),

Continue reading Intersection and sum of vector subspaces →

Algebra

Two non similar matrices having same minimal and characteristic polynomials

Leave a comment

Consider a square matrix \(A\) of dimension \(n \ge 1\) over a field \(\mathbb F\), i.e. \(A \in \mathcal M_n(\mathbb F)\). Results discuss below are true for any field \(\mathbb F\), in particular for \(\mathbb F = \mathbb R\) or \(\mathbb F = \mathbb C\).

A polynomial \(P \in \mathbb F[X]\) is called a vanishing polynomial for \(A\) if \(P(A) = 0\). If the matrix \(B\) is similar to \(B\) (which means that \(B=Q^{-1} A Q\) for some invertible matrix \(Q\)), and the polynomial \(P\) vanishes at \(A\) then \(P\) also vanishes at \(B\). This is easy to prove as we have \(P(B)=P(Q^{-1} A Q)=Q^{-1} P(A) Q\).

In particular, two similar matrices have the same minimal and characteristic polynomials.

Is the converse true? Are two matrices having the same minimal and characteristic polynomials similar? Continue reading Two non similar matrices having same minimal and characteristic polynomials →

Topology

Two algebraically complemented subspaces that are not topologically complemented

Leave a comment

We give here an example of a two complemented subspaces \(A\) and \(B\) that are not topologically complemented.

For this, we consider a vector space of infinite dimension equipped with an inner product. We also suppose that \(E\) is separable. Hence, \(E\) has an orthonormal basis \((e_n)_{n \in \mathbb N}\).

Let \(a_n=e_{2n}\) and \(b_n=e_{2n}+\frac{1}{2n+1} e_{2n+1}\). We denote \(A\) and \(B\) the closures of the linear subspaces generated by the vectors \((a_n)\) and \((b_n)\) respectively. We consider \(F=A+B\) and prove that \(A\) and \(B\) are complemented subspaces in \(F\), but not topologically complemented. Continue reading Two algebraically complemented subspaces that are not topologically complemented →

Algebra

A vector space written as a finite union of proper subspaces

Leave a comment

We raise here the following question: “can a vector space \(E\) be written as a finite union of proper subspaces”?

Let’s consider the simplest case, i.e. writing \(E= V_1 \cup V_2\) as a union of two proper subspaces. By hypothesis, one can find two non-zero vectors \(v_1,v_2\) belonging respectively to \(V_1 \setminus V_2\) and \(V_2 \setminus V_1\). The relation \(v_1+v_2 \in V_1\) leads to the contradiction \(v_2 = (v_1+v_2)-v_1 \in V_1\) while supposing \(v_1+v_2 \in V_2\) leads to the contradiction \(v_1 = (v_1+v_2)-v_2 \in V_2\). Therefore, a vector space can never be written as a union of two proper subspaces.

We now analyze if a vector space can be written as a union of \(n \ge 3\) proper subspaces. We’ll see that it is impossible when \(E\) is a vector space over an infinite field. But we’ll describe a counterexample of a vector space over the finite field \(\mathbb{Z}_2\) written as a union of three proper subspaces. Continue reading A vector space written as a finite union of proper subspaces →