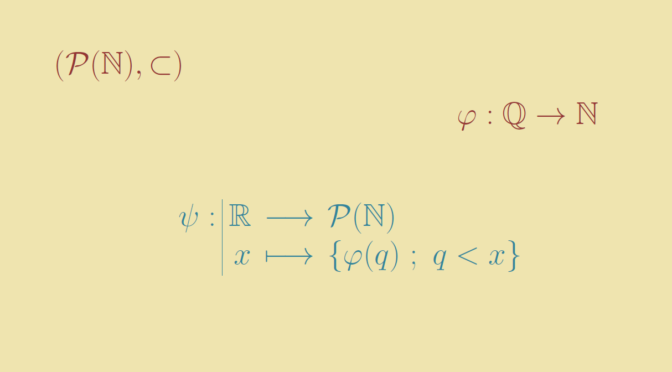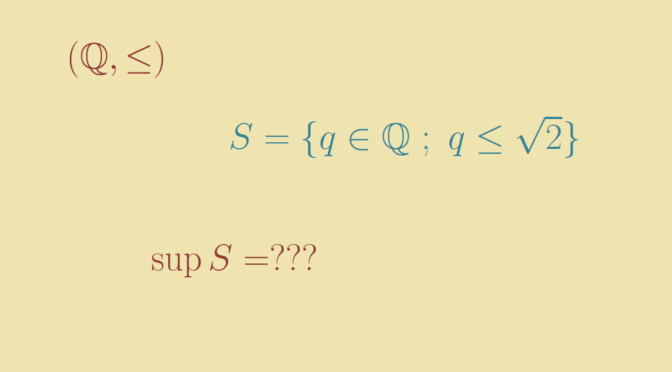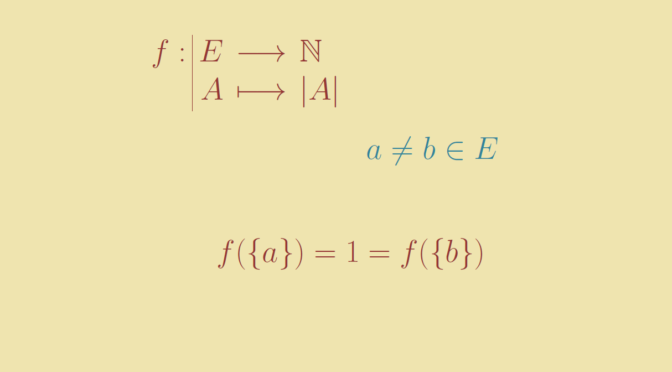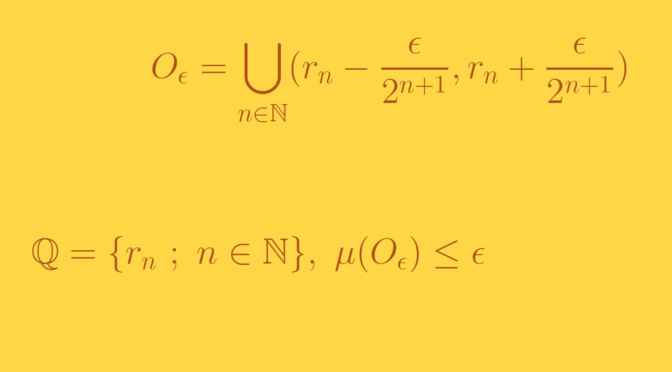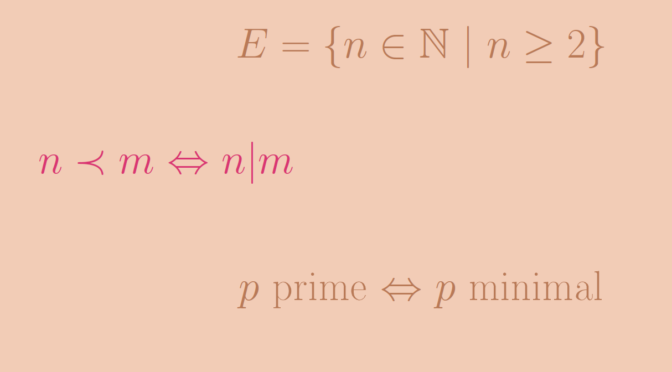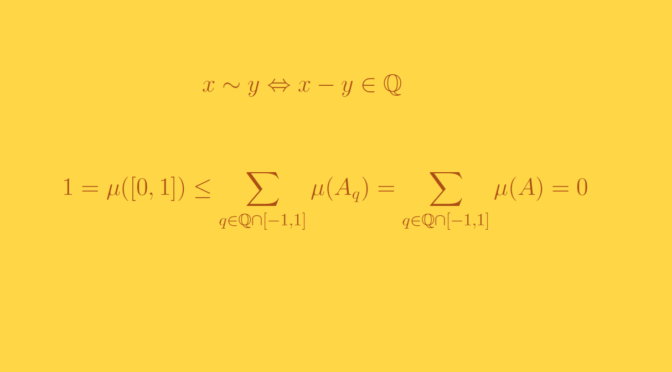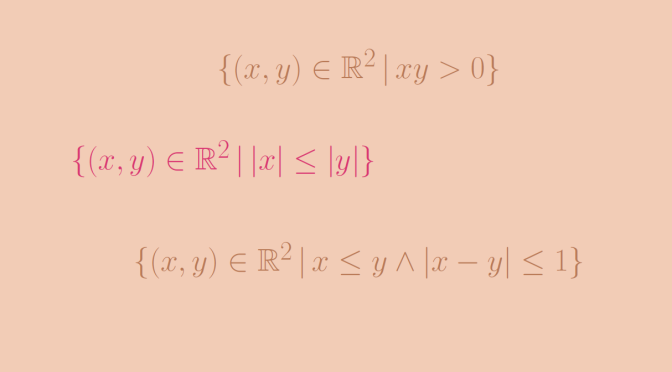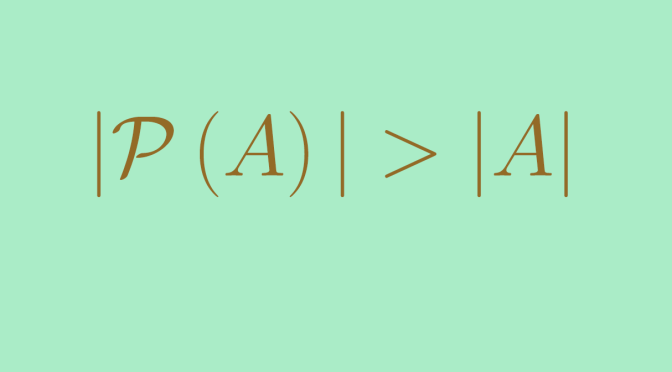Tag Archives: set-theory

Set Theory

An uncountable chain of subsets of the natural numbers

Leave a comment

Consider the set \(\mathcal P(\mathbb N)\) of the subsets of the natural integers \(\mathbb N\). \(\mathcal P(\mathbb N)\) is endowed with the strict order \(\subset\). Let’s have a look to the chains of \((\mathcal P(\mathbb N),\subset)\), i.e. to the totally ordered subsets \(S \subset \mathcal P(\mathbb N)\).

Some finite chains

It is easy to produce some finite chains like \(\{\{1\}, \{1,2\},\{1,2,3\}\}\) or one with a length of size \(n\) where \(n\) is any natural number like \[
\{\{1\}, \{1,2\}, \dots, \{1,2, \dots, n\}\}\] or \[
\{\{1\}, \{1,2^2\}, \dots, \{1,2^2, \dots, n^2\}\}\]

Some infinite countable chains

It’s not much complicated to produce some countable infinite chains like \[
\{\{1 \},\{1,2 \},\{1,2,3\},…,\mathbb{N}\}\] or \[
\{\{5 \},\{5,6 \},\{5,6,7\},…,\mathbb N \setminus \{1,2,3,4\} \}\]

Let’s go further and define a one-to-one map from the real interval \([0,1)\) into the set of countable chains of \((\mathcal P(\mathbb N),\subset)\). For \(x \in [0,1)\) let \(\displaystyle x = \sum_{i=1}^\infty x_i 2^{-i}\) be its binary representation. For \(n \in \mathbb N\) we define \(S_n(x) = \{k \in \mathbb N \ ; \ k \le n \text{ and } x_k = 1\}\). It is easy to verify that \(\left(S_n(x))_{n \in \mathbb N}\right)\) is a countable chain of \((\mathcal P(\mathbb N),\subset)\) and that \(\left(S_n(x))\right) \neq \left(S_n(x^\prime))\right)\) for \(x \neq x^\prime\).

What about defining an uncountable chain? Continue reading An uncountable chain of subsets of the natural numbers →

Set Theory

Around bounded sets, greatest element and supremum

Leave a comment

Consider a linearly ordered set \((X, \le)\) and a subset \(S \subseteq X\). Let’s recall some definitions:

  • \(S\) is bounded above if there exists an element \(k \in X\) such that \(k \ge s\) for all \(s \in S\).
  • \(g\) is a greatest element of \(S\) is \(g \in S\) and \(g \ge s\) for all \(s \in S\). \(l\) is a lowest element of \(S\) is \(l \in S\) and \(l \le s\) for all \(s \in S\).
  • \(a\) is an supremum of \(S\) if it is the least element in \(X\) that is greater than or equal to all elements of \(S\).

Subsets with a supremum but no greatest element

Let’s give examples of subsets having a supremum but no greatest element. First consider the ordered set \((\mathbb R, \le)\) and the subset \(S=\{ q \in \mathbb Q \ ; \ q \le \sqrt{2}\}\). \(S\) is bounded above by \(2\). \(\sqrt{2}\) is a supremum of \(S\) as we have \(q \le \sqrt{2}\) for all \(q \in S\) and as for \(b < \sqrt{2}\), it exists \(q \in \mathbb Q\) such that \(b < q < \sqrt{2}\) because \(\mathbb Q\) is dense in \(\mathbb R\). However \(S\) doesn't have a greatest element because \(\sqrt{2}\) is an irrational number.

For our second example we take \(X = \mathbb N \times \mathbb N\) ordered lexicographically by \(\preceq\). The subset \(S=\{(0,n) \ ; \ n \in \mathbb N\}\) is bounded above by \((2,0)\). Moreover \((1,0)\) is a supremum. But \(S\) doesn’t have a greatest element as for \((0,n) \in S\) we have \((0,n) \prec (0,n+1)\).

Bounded above subsets with no supremum

Leveraging the examples above, we take \((X, \le) = (\mathbb Q, \le)\) and \(S=\{ q \in \mathbb Q \ ; \ q \le \sqrt{2}\}\). \(S\) is bounded above, by \(2\) for example. However \(S\) doesn’t have a supremum because \(\sqrt{2} \notin \mathbb Q\).

Another example is the set \(X = \mathbb N \times \mathbb Z\) ordered lexicographically by \(\preceq\). The subset \(S=\{(0,n) \ ; \ n \in \mathbb N\}\) is bounded above by \((2,0)\) but has no supremum. Indeed, the elements greater or equal to all the elements of \(S\) are the elements \((a,b)\) with \(a \ge 1\). However \((a,b)\) with \(a \ge 1\) cannot be a supremum of \(S\), as \((a,b-1) \prec (a,b)\) and \((a,b-1)\) is greater than all the elements of \(S\).

Set Theory

A strictly increasing map that is not one-to-one

Leave a comment

Consider two partially ordered sets \((E,\le)\) and \((F,\le)\) and a strictly increasing map \(f : E \to F\). If the order \((E,\le)\) is total, then \(f\) is one-to-one. Indeed for distinct elements \(x,y \in E\), we have either \(x < y\) or \(y < x\) and consequently \(f(x) < f(y)\) or \(f(y) < f(x)\). Therefore \(f(x)\) and \(f(y)\) are different. This is not true anymore for a partial order \((E,\le)\). We give a counterexample.

Consider a finite set \(E\) having at least two elements and partially ordered by the inclusion. Let \(f\) be the map defined on the powerset \(\wp(E)\) that maps \(A \subseteq E\) to its cardinal \(\vert A \vert \). \(f\) is obviously strictly increasing. However \(f\) is not one-to-one as for distincts elements \(a,b \in E\) we have \[
f(\{a\}) = 1 = f(\{b\})\]

Set Theory

Small open sets containing the rationals

Leave a comment

The set \(\mathbb Q\) of the rational number is countable infinite and dense in \(\mathbb R\). You can have a look here on a way to build a bijective map between \(\mathbb N\) and \(\mathbb Q\).

Now given \(\epsilon > 0\), can one find an open set \(O_\epsilon\) of measure less than \(\epsilon\) with \(\mathbb Q \subseteq O_\epsilon\)?

The answer is positive. Let’s denote \[
O_\epsilon = \bigcup_{n \in \mathbb N} (r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\] where \((r_n)_{n \in \mathbb N}\) is an enumeration of the rationals. Obviously \(\mathbb Q \subseteq O_\epsilon\). Using countable subadditivity of Lebesgue measure \(\mu\), we get:
\begin{align*}
\mu(O_\epsilon) &\le \sum_{n \in \mathbb N} \mu((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}}))\\
&= \sum_{n \in \mathbb N} \frac{2 \epsilon}{2^{n+1}} = \sum_{n \in \mathbb N} \frac{\epsilon}{2^n} = \epsilon
\end{align*}

Therefore we’re done. Some additional comments:

  • While Lebesgue measure of the reals is infinite and the rationals are dense in the reals, we can include the rationals in an open set of measure as small as desired!
  • The open segments \((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\) are overlapping. Hence \(\mu(O_\epsilon)\) is strictly less than \(\epsilon\).
Set Theory

A partially ordered set having multiple minimal elements

Leave a comment

Let’s consider a partially ordered set (or poset) \(E\).

If \(E\) is totally ordered, \(E\) has at most one minimal element. If \(E\) is not totally ordered, \(E\) can have multiple minimal elements. We provide an example for the set \(E=\{n \in \mathbb N \ | \ n \ge 2\}\). For two natural numbers \(n\) and \(m\), we write \(n|m\) if \(n\) divides \(m\). One easily sees that this yields a partial order.

The minimal elements of \(E\) are the elements not having divisors, this is the case for all prime numbers \(p \in E\).

\(E\) has an infinite number of minimal elements which are the prime numbers.

Set Theory

A non-measurable set

Leave a comment

We describe here a non-measurable subset of the segment \(I=[0,1] \subset \mathbb R\).

Let’s define on \(I\) an equivalence relation by \(x \sim y\) if and only if \(x-y \in \mathbb Q\). The equivalence relation \(\sim\) induces equivalence classes on \(I\). For \(x \in I\), it’s equivalence class \([x]\) is \([x] = \{y \in I \ : \ y-x \in \mathbb Q\}\). By the Axiom of Choice, we can form a set \(A\) by selecting a single point from each equivalence class.

We claim that the set \(A\) is not Lebesgue measurable.

For all \(q \in \mathbb Q\) we denote \(A_q = \{q+x \ : x \in A\}\). Let’s take \(p,q \in \mathbb Q\). If it exists \(z \in A_p \cap A_q\), it means that there exist \(u,v \in A\) such that
\[z= p+u=q+v\] hence \(u-v=q-p=0\) as \(u,v\) are supposed to be unique representatives of the classes of the equivalence relation \(\sim\). Finally if \(p,q\) are distincts, \(A_p \cap A_q = \emptyset\).

As Lebesgue measure \(\mu\) is translation invariant, we have for \(q \in \mathbb Q \cap [0,1]\) : \(\mu(A) = \mu(A_q)\) and also \(A_q \subset [0,2]\). Hence if we denote
\[B = \bigcup_{q \in \mathbb Q \cap [0,1]} A_q\] we have \(B \subset [0,2]\). If we suppose that \(A\) is measurable, we get
\[\mu(B) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A) \le 2\] by countable additivity of Lebesgue measure (the set \(\mathbb Q \cap [0,1]\) being countable infinite). This implies \(\mu(A) = 0\).

Let’s prove now that
\[[0,1] \subset \bigcup_{q \in \mathbb Q \cap [-1,1]} A_q\] For \(z \in [0,1]\), there exists \(u \in A\) such that \(z \in [u]\). As \(A \subset [0,1]\), we have \(q = z-u \in \mathbb Q\) and \(-1 \le q \le 1\). And \(z=q+u\) means that \(z \in A_q\). This proves the inclusion. However the inclusion implies the contradiction
\[1 = \mu([0,1]) \le \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A) =0\]

Finally \(A\) is not Lebesgue measurable.

Set Theory

Around binary relations on sets

Leave a comment

We are considering here binary relations on a set \(A\). Let’s recall that a binary relation \(R\) on \(A\) is a subset of the cartesian product \(R \subseteq A \times A\). The statement \((x,y) \in R\) is read as \(x\) is \(R\)-related to \(y\) and also denoted by \(x R y \).

Some importants properties of a binary relation \(R\) are:

reflexive
For all \(x \in A\) it holds \(x R y\)
irreflexive
For all \(x \in A\) it holds not \(x R y\)
symmetric
For all \(x,y \in A\) it holds that if \(x R y\) then \(y R x\)
antisymmetric
For all \(x,y \in A\) if \(x R y\) and \(y R x\) then \(x=y\)
transitive
For all \(x,y,z \in A\) it holds that if \(x R y\) and \(y R z\) then \(x R z\)

A relation that is reflexive, symmetric and transitive is called an equivalence relation. Let’s see that being reflexive, symmetric and transitive are independent properties.

Symmetric and transitive but not reflexive

We provide two examples of such relations. For the first one, we take for \(A\) the set of the real numbers \(\mathbb R\) and the relation \[R = \{(x,y) \in \mathbb R^2 \, | \, xy >0\}.\] \(R\) is symmetric as the multiplication is also symmetric. \(R\) is also transitive as if \(xy > 0\) and \(yz > 0\) you get \(xy^2 z >0\). And as \(y^2 > 0\), we have \(xz > 0\) which means that \(x R z\). However, \(R\) is not reflexive as \(0 R 0\) doesn’t hold.

For our second example, we take \(A= \mathbb N\) and \(R=\{(1,1)\}\). It is easy to verify that \(R\) is symmetric and transitive. However \(R\) is not reflexive as \(n R n\) doesn’t hold for \(n \neq 1\). Continue reading Around binary relations on sets →

Set Theory

There is no greatest cardinal

Leave a comment

We have seen in this article several sets that are infinite and countable. Namely, the set of natural numbers \(\mathbb N\), the set of integers \(\mathbb Z\), the set of rational numbers \(\mathbb Q\). We have seen that the product \(\mathbb N \times \mathbb N\) is also countable. The question then arises, “Are all infinite sets countable?”.

The answer is negative and we prove that \(\mathbb R\) is not countable.

The set of all reals \(\mathbb R\) is not countable

Suppose for the sake of contradiction that \(\mathbb R\) is countable and that \(\mathbb R = \{x_n \ | \ n \in \mathbb N\}\), the \(x_n\) being all distinct. We build by induction two sequences \((a_n)_{n \in \mathbb N}\) increasing and \((b_n)_{n \in \mathbb N}\) decreasing such that:

  • \(a_n < b_n\) for all \(n \in \mathbb N\),
  • \(\vert a_n – b_n \vert \) converges to zero,
  • and \(x_n \notin [a_{n+1},b_{n+1}]\).

Continue reading There is no greatest cardinal →

Set Theory

Counterexamples around cardinality (part 2)

3 Comments

I follow on here from the initial article on cardinality. In that article, we have seen that \(\mathbb N\) contains an infinite countable subset whose complement is also infinite. Namely the subsets of even and odd integers.

Let’s now consider the set \(\mathbb N \times \mathbb N\). \(\mathbb N \times \mathbb N\) contains a countable infinite number of copies of \(\mathbb N\), as for all \(i \in \mathbb N\), \(\{i\} \times \mathbb N \subset \mathbb N \times \mathbb N\). Surprisingly, it is however possible to define a bijection between \(\mathbb N \times \mathbb N\) and \(\mathbb N\).

\(\mathbb N \times \mathbb N\) is equinumerous to \(\mathbb N\)

Consider the map \[\begin{array}{l|rcl}
\varphi : & \mathbb N \times \mathbb N & \longrightarrow & \mathbb N\\
& (n,m) & \longmapsto & 2^{n-1} (2m-1) \end{array}\] \(\varphi\) is one-to-one. Suppose that \(2^{n_1-1} (2m_1-1) = 2^{n_2-1} (2m_2-1)\). If \(n_1=1\), we must also have \(n_2=1\) as \(2 m_1 – 1\) is odd. That implies \((n_1,m_1)=(n_2,m_2)\). Let’s now suppose \(n_1 >1\). According to Euclid’s lemma, \(2^{n_1-1}\) divides \(2^{n_2-1}\) as \(2^{n_1-1}\) is even and \(2m_2 – 1\) odd. By symmetry \(2^{n_2-1}\) also divides \(2^{n_1-1}\). Finally, \(2^{n_1 – 1} = 2^{n_2 – 1}\), \(n_1 = n_2\) and consequently \(m_1 = m_2\). Continue reading Counterexamples around cardinality (part 2) →

Set Theory

Counterexamples around cardinality (part 1)

1 Comment

In mathematics, the cardinality of a set is a measure of the “number of elements of the set”. We denote by \(|A|\) the cardinality of the set \(A\). We say that \(A\) and \(B\) have the same cardinality if there exists a bijection from \(A\) onto \(B\). Such sets said to be equinumerous.

The finite sets satisfy the property that if \(A \subset B\) and \(A\) and \(B\) have the same cardinality then \(A=B\). For example take \(A=\{2,5,42\}\). If \(A \subset B\) and \(B\) has more elements than \(A\), a bijection \(f\) from \(A\) to \(B\) cannot exist as an element in \(B \setminus \{f(2),f(5),f(42)\}\) won’t have an inverse image under \(f\).

This becomes false for infinite sets. Let’s give some examples.

Proper subsets of \(\mathbb N\) equinumerous to \(\mathbb N\)

The set \(A\) of the positive even integers is strictly included in \(\mathbb N\): there exist odd positive integers! However, \(A\) is equinumerous to \(\mathbb N\). The map \(f : n \to 2n\) is a bijection from \(A\) onto \(\mathbb N\).

For our second example, consider the set \(\mathbb P\) of prime numbers. We recall that \(\mathbb P\) is infinite. The proof is quite simple by contradiction. Suppose that there is only a finite number \(\{p_1, \dots, p_n\}\) of prime numbers and consider the number \(N = p_1 p_2 \cdots p_n + 1\). As a consequence of the fundamental theorem of arithmetic, a prime \(q\) divides \(N\). However \(q \notin \{p_1, \dots, p_n\}\) as this would imply \(q\) divides \(1\). From there, we can define by induction a bijection from \(\mathbb N\) onto \(\mathbb P\) by defining \[f(n)=\begin{cases}
2 & \text{for } n=1\\
\min (\mathbb P \setminus \{p_1, \dots, p_n\}) & \text{else }
\end{cases}\] Continue reading Counterexamples around cardinality (part 1) →