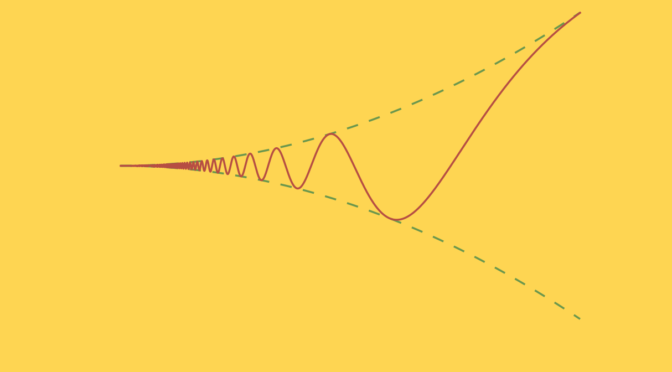
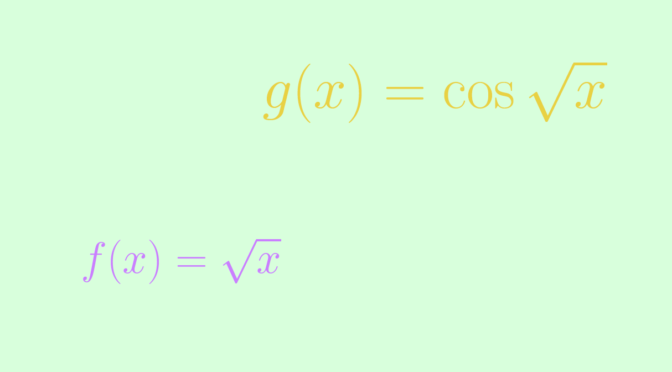Tag Archives: real-analysis

Analysis

A differentiable real function with unbounded derivative around zero

Leave a comment

Consider the real function defined on \(\mathbb R\)\[
f(x)=\begin{cases}
0 &\text{for } x = 0\\
x^2 \sin \frac{1}{x^2} &\text{for } x \neq 0
\end{cases}\]

\(f\) is continuous and differentiable on \(\mathbb R\setminus \{0\}\). For \(x \in \mathbb R\) we have \(\vert f(x) \vert \le x^2\), which implies that \(f\) is continuous at \(0\). Also \[
\left\vert \frac{f(x)-f(0)}{x} \right\vert = \left\vert x \sin \frac{1}{x^2} \right\vert \le \vert x \vert\] proving that \(f\) is differentiable at zero with \(f^\prime(0) = 0\). The derivative of \(f\) for \(x \neq 0\) is \[
f^\prime(x) = \underbrace{2x \sin \frac{1}{x^2}}_{=g(x)}-\underbrace{\frac{2}{x} \cos \frac{1}{x^2}}_{=h(x)}\] On the interval \((-1,1)\), \(g(x)\) is bounded by \(2\). However, for \(a_k=\frac{1}{\sqrt{k \pi}}\) with \(k \in \mathbb N\) we have \(h(a_k)=2 \sqrt{k \pi} (-1)^k\) which is unbounded while \(\lim\limits_{k \to \infty} a_k = 0\). Therefore \(f^\prime\) is unbounded in all neighborhood of the origin.

Analysis

A Riemann-integrable map that is not regulated

Leave a comment

For a Banach space \(X\), a function \(f : [a,b] \to X\) is said to be regulated if there exists a sequence of step functions \(\varphi_n : [a,b] \to X\) converging uniformly to \(f\).

One can prove that a regulated function \(f : [a,b] \to X\) is Riemann-integrable. Is the converse true? The answer is negative and we provide below an example of a Riemann-integrable real function that is not regulated. Let’s first prove following theorem.

THEOREM A bounded function \(f : [a,b] \to \mathbb R\) that is (Riemann) integrable on all intervals \([c, b]\) with \(a < c < b\) is integrable on \([a,b]\).

PROOF Take \(M > 0\) such that for all \(x \in [a,b]\) we have \(\vert f(x) \vert < M\). For \(\epsilon > 0\), denote \(c = \inf(a + \frac{\epsilon}{4M},b + \frac{b-a}{2})\). As \(f\) is supposed to be integrable on \([c,b]\), one can find a partition \(P\): \(c=x_1 < x_2 < \dots < x_n =b\) such that \(0 \le U(f,P) - L(f,P) < \frac{\epsilon}{2}\) where \(L(f,P),U(f,P)\) are the lower and upper Darboux sums. For the partition \(P^\prime\): \(a= x_0 < c=x_1 < x_2 < \dots < x_n =b\), we have \[ \begin{aligned} 0 \le U(f,P^\prime) - L(f,P^\prime) &\le 2M(c-a) + \left(U(f,P) - L(f,P)\right)\\ &< 2M \frac{\epsilon}{4M} + \frac{\epsilon}{2} = \epsilon \end{aligned}\] We now prove that the function \(f : [0,1] \to [0,1]\) defined by \[ f(x)=\begin{cases} 1 &\text{ if } x \in \{2^{-k} \ ; \ k \in \mathbb N\}\\ 0 &\text{otherwise} \end{cases}\] is Riemann-integrable (that follows from above theorem) and not regulated. Let's prove it. If \(f\) was regulated, there would exist a step function \(g\) such that \(\vert f(x)-g(x) \vert < \frac{1}{3}\) for all \(x \in [0,1]\). If \(0=x_0 < x_1 < \dots < x_n=1\) is a partition associated to \(g\) and \(c_1\) the value of \(g\) on the interval \((0,x_1)\), we must have \(\vert 1-c_1 \vert < \frac{1}{3}\) as \(f\) takes (an infinite number of times) the value \(1\) on \((0,x_1)\). But \(f\) also takes (an infinite number of times) the value \(0\) on \((0,x_1)\). Hence we must have \(\vert c_1 \vert < \frac{1}{3}\). We get a contradiction as those two inequalities are not compatible.

Analysis

A discontinuous midpoint convex function

Leave a comment

Let’s recall that a real function \(f: \mathbb R \to \mathbb R\) is called convex if for all \(x, y \in \mathbb R\) and \(\lambda \in [0,1]\) we have \[
f((1- \lambda) x + \lambda y) \le (1- \lambda) f(x) + \lambda f(y)\] \(f\) is called midpoint convex if for all \(x, y \in \mathbb R\) \[
f \left(\frac{x+y}{2}\right) \le \frac{f(x)+f(y)}{2}\] One can prove that a continuous midpoint convex function is convex. Sierpinski proved the stronger theorem, that a real-valued Lebesgue measurable function that is midpoint convex will be convex.

Can one find a discontinuous midpoint convex function? The answer is positive but requires the Axiom of Choice. Why? Because Robert M. Solovay constructed a model of Zermelo-Fraenkel set theory (ZF), exclusive of the axiom of choice where all functions are Lebesgue measurable. Hence convex according to Sierpinski theorem. And one knows that convex functions defined on \(\mathbb R\) are continuous.

Referring to my previous article on the existence of discontinuous additive map, let’s use a Hamel basis \(\mathcal B = (b_i)_{i \in I}\) of \(\mathbb R\) considered as a vector space on \(\mathbb Q\). Take \(i_1 \in I\), define \(f(i_1)=1\) and \(f(i)=0\) for \(i \in I\setminus \{i_1\}\) and extend \(f\) linearly on \(\mathbb R\). \(f\) is midpoint convex as it is linear. As the image of \(\mathbb R\) under \(f\) is \(\mathbb Q\), \(f\) is discontinuous as explained in the discontinuous additive map counterexample.

Moreover, \(f\) is unbounded on all open real subsets. By linearity, it is sufficient to prove that \(f\) is unbounded around \(0\). Let’s consider \(i_1 \neq i_2 \in I\). \(G= b_{i_1} \mathbb Z + b_{i_2} \mathbb Z\) is a proper subgroup of the additive \(\mathbb R\) group. Hence \(G\) is either dense of discrete. It cannot be discrete as the set of vectors \(\{b_1,b_2\}\) is linearly independent. Hence \(G\) is dense in \(\mathbb R\). Therefore, one can find a non vanishing sequence \((x_n)_{n \in \mathbb N}=(q_n^1 b_{i_1} + q_n^2 b_{i_2})_{n \in \mathbb N}\) (with \((q_n^1,q_n^2) \in \mathbb Q^2\) for all \(n \in \mathbb N\)) converging to \(0\). As \(\{b_1,b_2\}\) is linearly independent, this implies \(\vert q_n^1 \vert, \vert q_n^2 \vert \underset{n\to+\infty}{\longrightarrow} \infty\) and therefore \[
\lim\limits_{n \to \infty} \vert f(x_n) \vert = \lim\limits_{n \to \infty} \vert f(q_n^1 b_{i_1} + q_n^2 b_{i_2}) \vert = \lim\limits_{n \to \infty} \vert q_n^1 \vert = \infty.\]

Analysis

A positive smooth function with all derivatives vanishing at zero

Leave a comment

Let’s consider the set \(\mathcal C^\infty(\mathbb R)\) of real smooth functions, i.e. functions that have derivatives of all orders on \(\mathbb R\).

Does a positive function \(f \in \mathcal C^\infty(\mathbb R)\) with all derivatives vanishing at zero exists?

Such a map \(f\) cannot be expandable in power series around zero, as it would vanish in a neighborhood of zero. However, the answer to our question is positive and we’ll prove that \[
f(x) = \left\{\begin{array}{lll}
e^{-\frac{1}{x^2}} &\text{if} &x \neq 0\\
0 &\text{if} &x = 0 \end{array}\right. \] provides an example.

\(f\) is well defined and positive for \(x \neq 0\). As \(\lim\limits_{x \to 0} -\frac{1}{x^2} = -\infty\), we get \(\lim\limits_{x \to 0} f(x) = 0\) proving that \(f\) is continuous on \(\mathbb R\). Let’s prove by induction that for \(x \neq 0\) and \(n \in \mathbb N\), \(f^{(n)}(x)\) can be written as \[
f^{(n)}(x) = \frac{P_n(x)}{x^{3n}}e^{-\frac{1}{x^2}}\] where \(P_n\) is a polynomial function. The statement is satisfied for \(n = 1\) as \(f^\prime(x) = \frac{2}{x^3}e^{-\frac{1}{x^2}}\). Suppose that the statement is true for \(n\) then \[
f^{(n+1)}(x)=\left[\frac{P_n^\prime(x)}{x^{3n}} – \frac{3n P_n(x)}{x^{3n+1}}+\frac{2 P_n(x)}{x^{3n+3}}\right] e^{-\frac{1}{x^2}}\] hence the statement is also true for \(n+1\) by taking \(P_{n+1}(x)=
x^3 P_n^\prime(x) – 3n x^2 P_n(x) + 2 P_n(x)\). Which concludes our induction proof.

Finally, we have to prove that for all \(n \in \mathbb N\), \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\). For that, we use the power expansion of the exponential map \(e^x = \sum_{n=0}^\infty \frac{x^n}{n!}\). For \(x \neq 0\), we have \[
\left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} \ge \frac{\vert x \vert^{3n}}{(2n)! \vert x \vert ^{4n}} = \frac{1}{(2n)! \vert x \vert^n}\] Therefore \(\lim\limits_{x \to 0} \left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} = \infty\) and \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\) as \(f^{(n)}(x) = \frac{P_n(x)}{x^{3n} e^{\frac{1}{x^2}}}\) with \(P_n\) a polynomial function.

Analysis

Counterexample around L’Hôpital’s rule

Leave a comment

Let us consider two differentiable functions \(f\) and \(g\) defined in an open interval \((a,b)\), where \(b\) might be \(\infty\). If
\[\lim\limits_{x \to b^-} f(x) = \lim\limits_{x \to b^-} g(x) = \infty\] and if \(g^\prime(x) \neq 0\) in some interval \((c,b)\), then a version of l’Hôpital’s rule states that \(\lim\limits_{x \to b^-} \frac{f^\prime(x)}{g^\prime(x)} = L\) implies \(\lim\limits_{x \to b^-} \frac{f(x)}{g(x)} = L\).

We provide a counterexample when \(g^\prime\) vanishes in all neighborhood of \(b\). The counterexample is due to the Austrian mathematician Otto Stolz.

We take \((0,\infty)\) for the interval \((a,b)\) and \[
\begin{cases}
f(x) &= x + \cos x \sin x\\
g(x) &= e^{\sin x}(x + \cos x \sin x)
\end{cases}\] which derivatives are \[
\begin{cases}
f^\prime(x) &= 2 \cos^2 x\\
g^\prime(x) &= e^{\sin x} \cos x (x + \cos x \sin x + 2 \cos x)
\end{cases}\] We have \[
\lim\limits_{x \to \infty} \frac{f^\prime(x)}{g^\prime(x)} = \lim\limits_{x \to \infty} \frac{2 \cos x}{e^{\sin x} (x + \cos x \sin x + 2 \cos x)} = 0,\] however \[
\frac{f(x)}{g(x)} = \frac{1}{e^{\sin x}}\] doesn’t have any limit at \(\infty\) as it oscillates between \(\frac{1}{e}\) and \(e\).

Analysis

On limit at infinity of functions and their derivatives

Leave a comment

We consider continuously differentiable real functions defined on \((0,\infty)\) and the limits \[
\lim\limits_{x \to \infty} f(x) \text{ and } \lim\limits_{x \to \infty} f^\prime(x).\]

A map \(f\) such that \(\lim\limits_{x \to \infty} f(x) = \infty\) and \(\lim\limits_{x \to \infty} f^\prime(x) = 0\)

Consider the map \(f : x \mapsto \sqrt{x}\). It is clear that \(\lim\limits_{x \to \infty} f(x) = \infty\). As \(f^\prime(x) = \frac{1}{2 \sqrt{x}}\), we have as announced \(\lim\limits_{x \to \infty} f^\prime(x) = 0\)

A bounded map \(g\) having no limit at infinity such that \(\lim\limits_{x \to \infty} g^\prime(x) = 0\)

One idea is to take an oscillating map whose wavelength is increasing to \(\infty\). Let’s take the map \(g : x \mapsto \cos \sqrt{x}\). \(g\) doesn’t have a limit at \(\infty\) as for \(n \in \mathbb N\), we have \(g(n^2 \pi^2) = \cos n \pi = (-1)^n\). However, the derivative of \(g\) is \[
g^\prime(x) = – \frac{\sin \sqrt{x}}{2 \sqrt{x}},\] and as \(\vert g^\prime(x) \vert \le \frac{1}{2 \sqrt{x}}\) for all \(x \in (0,\infty)\), we have \(\lim\limits_{x \to \infty} g^\prime(x) = 0\).

Analysis

Limit points of real sequences

1 Comment

Let’s start by recalling an important theorem of real analysis:

THEOREM. A necessary and sufficient condition for the convergence of a real sequence is that it is bounded and has a unique limit point.

As a consequence of the theorem, a sequence having a unique limit point is divergent if it is unbounded. An example of such a sequence is the sequence \[
u_n = \frac{n}{2}(1+(-1)^n),\] whose initial values are \[
0, 1, 0, 2, 0, 3, 0, 4, 0, 5, 6, \dots\] \((u_n)\) is an unbounded sequence whose unique limit point is \(0\).

Let’s now look at sequences having more complicated limit points sets.

A sequence whose set of limit points is the set of natural numbers

Consider the sequence \((v_n)\) whose initial terms are \[
1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, \dots\] \((v_n)\) is defined as follows \[
v_n=\begin{cases}
1 &\text{ for } n= 1\\
n – \frac{k(k+1)}{2} &\text{ for } \frac{k(k+1)}{2} \lt n \le \frac{(k+1)(k+2)}{2}
\end{cases}\] \((v_n)\) is well defined as the sequence \((\frac{k(k+1)}{2})_{k \in \mathbb N}\) is strictly increasing with first term equal to \(1\). \((v_n)\) is a sequence of natural numbers. As \(\mathbb N\) is a set of isolated points of \(\mathbb R\), we have \(V \subseteq \mathbb N\), where \(V\) is the set of limit points of \((v_n)\). Conversely, let’s take \(m \in \mathbb N\). For \(k + 1 \ge m\), we have \(\frac{k(k+1)}{2} + m \le \frac{(k+1)(k+2)}{2}\), hence \[
u_{\frac{k(k+1)}{2} + m} = m\] which proves that \(m\) is a limit point of \((v_n)\). Finally the set of limit points of \((v_n)\) is the set of natural numbers.

Continue reading Limit points of real sequences →

Analysis

Continuity versus uniform continuity

Leave a comment

We consider real-valued functions.

A real-valued function \(f : I \to \mathbb R\) (where \(I \subseteq\) is an interval) is continuous at \(x_0 \in I\) when: \[(\forall \epsilon > 0) (\exists \delta > 0)(\forall x \in I)(\vert x- x_0 \vert \le \delta \Rightarrow \vert f(x)- f(x_0) \vert \le \epsilon).\] When \(f\) is continuous at all \(x \in I\), we say that \(f\) is continuous on \(I\).

\(f : I \to \mathbb R\) is said to be uniform continuity on \(I\) if \[(\forall \epsilon > 0) (\exists \delta > 0)(\forall x,y \in I)(\vert x- y \vert \le \delta \Rightarrow \vert f(x)- f(y) \vert \le \epsilon).\]

Obviously, a function which is uniform continuous on \(I\) is continuous on \(I\). Is the converse true? The answer is negative.

An (unbounded) continuous function which is not uniform continuous

The map \[
\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x^2 \end{array}\] is continuous. Let’s prove that it is not uniform continuous. For \(0 < x < y\) we have \[\vert f(x)-f(y) \vert = y^2-x^2 = (y-x)(y+x) \ge 2x (y-x)\] Hence for \(y-x= \delta >0\) and \(x = \frac{1}{\delta}\) we get
\[\vert f(x) -f(y) \vert \ge 2x (y-x) =2 > 1\] which means that the definition of uniform continuity is not fulfilled for \(\epsilon = 1\).

For this example, the function is unbounded as \(\lim\limits_{x \to \infty} x^2 = \infty\). Continue reading Continuity versus uniform continuity →

Analysis

No minimum at the origin but a minimum along all lines

Leave a comment

We look here at an example, from the Italian mathematician Giuseppe Peano of a real function \(f\) defined on \(\mathbb{R}^2\). \(f\) is having a local minimum at the origin along all lines passing through the origin, however \(f\) does not have a local minimum at the origin as a function of two variables.

The function \(f\) is defined as follows
\[\begin{array}{l|rcl}
f : & \mathbb{R}^2 & \longrightarrow & \mathbb{R} \\
& (x,y) & \longmapsto & f(x,y)=3x^4-4x^2y+y^2 \end{array}\] One can notice that \(f(x, y) = (y-3x^2)(y-x^2)\). In particular, \(f\) is strictly negative on the open set \(U=\{(x,y) \in \mathbb{R}^2 \ : \ x^2 < y < 3x^2\}\), vanishes on the parabolas \(y=x^2\) and \(y=3 x^2\) and is strictly positive elsewhere. Consider a line \(D\) passing through the origin. If \(D\) is different from the coordinate axes, the equation of \(D\) is \(y = \lambda x\) with \(\lambda > 0\). We have \[f(x, \lambda x)= x^2(\lambda-3x)(\lambda -x).\] For \(x \in (-\infty,\frac{\lambda}{3}) \setminus \{0\}\), \(f(x, \lambda x) > 0\) while \(f(0,0)=0\) which proves that \(f\) has a local minimum at the origin along the line \(D \equiv y – \lambda x=0\). Along the \(x\)-axis, we have \(f(x,0)=3 x^ 4\) which has a minimum at the origin. And finally, \(f\) also has a minimum at the origin along the \(y\)-axis as \(f(0,y)=y^2\).

However, along the parabola \(\mathcal{P} \equiv y = 2 x^2\) we have \(f(x,2 x^2)=-x^4\) which is strictly negative for \(x \neq 0\). As \(\mathcal{P}\) is passing through the origin, \(f\) assumes both positive and negative values in all neighborhood of the origin.

This proves that \(f\) does not have a minimum at \((0,0)\).

Analysis

Counterexamples around Fubini’s theorem

Leave a comment

We present here some counterexamples around the Fubini theorem.

We recall Fubini’s theorem for integrable functions:
let \(X\) and \(Y\) be \(\sigma\)-finite measure spaces and suppose that \(X \times Y\) is given the product measure. Let \(f\) be a measurable function for the product measure. Then if \(f\) is \(X \times Y\) integrable, which means that \(\displaystyle \int_{X \times Y} \vert f(x,y) \vert d(x,y) < \infty\), we have \[\int_X \left( \int_Y f(x,y) dy \right) dx = \int_Y \left( \int_X f(x,y) dx \right) dy = \int_{X \times Y} f(x,y) d(x,y)\] Let's see what happens when some hypothesis of Fubini's theorem are not fulfilled. Continue reading Counterexamples around Fubini’s theorem →