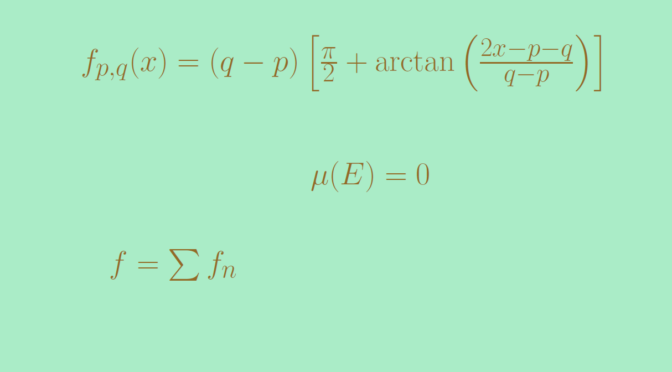Tag Archives: monotonic

Analysis

A strictly increasing continuous function that is differentiable at no point of a null set

Leave a comment

We build in this article a strictly increasing continuous function \(f\) that is differentiable at no point of a null set \(E\). The null set \(E\) can be chosen arbitrarily. In particular it can have the cardinality of the continuum like the Cantor null set.

A set of strictly increasing continuous functions

For \(p \lt q\) two real numbers, consider the function \[
f_{p,q}(x)=(q-p) \left[\frac{\pi}{2} + \arctan{\left(\frac{2x-p-q}{q-p}\right)}\right]\] \(f_{p,q}\) is positive and its derivative is \[
f_{p,q}^\prime(x) = \frac{2}{1+\left(\frac{2x-p-q}{q-p}\right)^2}\] which is always strictly positive. Hence \(f_{p,q}\) is strictly increasing. We also have \[
\lim\limits_{x \to -\infty} f_{p,q}(x) = 0 \text{ and } \lim\limits_{x \to \infty} f_{p,q}(x) = \pi(q-p).\] One can notice that for \(x \in (p,q)\), \(f_{p,q}^\prime(x) \gt 1\). Therefore for \(x, y \in (p,q)\) distinct we have according to the mean value theorem \(\frac{f_{p,q}(y)-f_{p,q}(x)}{y-x} \ge 1\).

Covering \(E\) with an appropriate set of open intervals

As \(E\) is a null set, for each \(n \in \mathbb N\) one can find an open set \(O_n\) containing \(E\) and measuring less than \(2^{-n}\). \(O_n\) can be written as a countable union of disjoint open intervals as any open subset of the reals. Then \(I=\bigcup_{m \in \mathbb N} O_m\) is also a countable union of open intervals \(I_n\) with \(n \in \mathbb N\). The sum of the lengths of the \(I_n\) is less than \(1\). Continue reading A strictly increasing continuous function that is differentiable at no point of a null set →

Analysis

A monotonic function whose points of discontinuity form a dense set

Leave a comment

Consider a compact interval \([a,b] \subset \mathbb R\) with \(a \lt b\). Let’s build an increasing function \(f : [a,b] \to \mathbb R\) whose points of discontinuity is an arbitrary dense subset \(D = \{d_n \ ; \ n \in \mathbb N\}\) of \([a,b]\), for example \(D = \mathbb Q \cap [a,b]\).

Let \(\sum p_n\) be a convergent series of positive numbers whose sum is equal to \(p\) and define \(\displaystyle f(x) = \sum_{d_n \le x} p_n\).

\(f\) is strictly increasing

For \(a \le x \lt y \le b\) we have \[
f(y) – f(x) = \sum_{x \lt d_n \le y} p_n \gt 0\] as the \(p_n\) are positive and dense so it exists \(p_m \in (x, y]\).

\(f\) is right-continuous on \([a,b]\)

We pick-up \(x \in [a,b]\). For any \(\epsilon \gt 0\) is exists \(N \in \mathbb N\) such that \(0 \lt \sum_{n \gt N} p_n \lt \epsilon\). Let \(\delta > 0\) be so small that the interval \((x,x+\delta)\) doesn’t contain any point in the finite set \(\{p_1, \dots, p_N\}\). Then \[
0 \lt f(y) – f(x) \le \sum_{n \gt N} p_n \lt \epsilon,\] for any \(y \in (x,x+\delta)\) proving the right-continuity of \(f\) at \(x\). Continue reading A monotonic function whose points of discontinuity form a dense set →

Analysis

A function whose derivative at 0 is one but which is not increasing near 0

Leave a comment

From the mean value theorem, a real function whose derivative is strictly positive at every point of an interval is strictly increasing. In particular, a continuously differentiable function \(f\) defined in a non-degenerate interval \(I\) with a strictly positive derivative at a point \(a\) of the interval is strictly increasing near that point. For the proof, we just have to notice that as \(f^\prime\) is continuous and \(f^\prime(a) > 0\), \(f^\prime\) is strictly positive within an interval \(J \subset I\) containing \(a\). By the mean value theorem, \(f\) is strictly increasing on \(J\).

We now suppose that \(f\) is differentiable on an interval \(I\) containing \(0\) with \(f^\prime(0)>0\). For \(x>0\) sufficiently close to zero we have \(\displaystyle \frac{f(x)-f(0)}{x-0} > \frac{f^\prime(0)}{2}>0\), hence \(f(x)>f(0)\). But that doesn’t imply that \(f\) is strictly increasing in a neighborhood of zero. Let’s prove it with a counterexample. Continue reading A function whose derivative at 0 is one but which is not increasing near 0 →