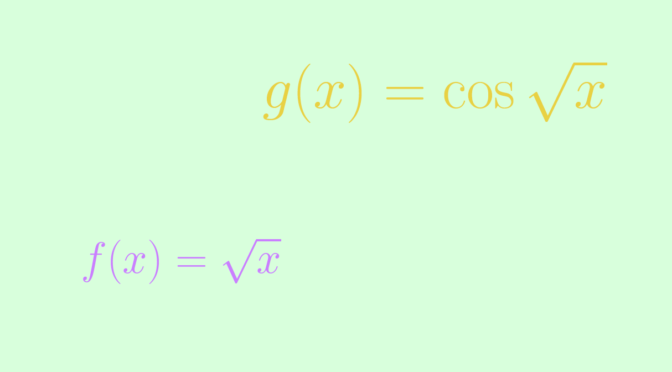Tag Archives: maps

Analysis

On limit at infinity of functions and their derivatives

Leave a comment

We consider continuously differentiable real functions defined on \((0,\infty)\) and the limits \[
\lim\limits_{x \to \infty} f(x) \text{ and } \lim\limits_{x \to \infty} f^\prime(x).\]

A map \(f\) such that \(\lim\limits_{x \to \infty} f(x) = \infty\) and \(\lim\limits_{x \to \infty} f^\prime(x) = 0\)

Consider the map \(f : x \mapsto \sqrt{x}\). It is clear that \(\lim\limits_{x \to \infty} f(x) = \infty\). As \(f^\prime(x) = \frac{1}{2 \sqrt{x}}\), we have as announced \(\lim\limits_{x \to \infty} f^\prime(x) = 0\)

A bounded map \(g\) having no limit at infinity such that \(\lim\limits_{x \to \infty} g^\prime(x) = 0\)

One idea is to take an oscillating map whose wavelength is increasing to \(\infty\). Let’s take the map \(g : x \mapsto \cos \sqrt{x}\). \(g\) doesn’t have a limit at \(\infty\) as for \(n \in \mathbb N\), we have \(g(n^2 \pi^2) = \cos n \pi = (-1)^n\). However, the derivative of \(g\) is \[
g^\prime(x) = – \frac{\sin \sqrt{x}}{2 \sqrt{x}},\] and as \(\vert g^\prime(x) \vert \le \frac{1}{2 \sqrt{x}}\) for all \(x \in (0,\infty)\), we have \(\lim\limits_{x \to \infty} g^\prime(x) = 0\).

Algebra

Non linear map preserving Euclidean norm

Leave a comment

Let \(V\) be a real vector space endowed with an Euclidean norm \(\Vert \cdot \Vert\).

A bijective map \( T : V \to V\) that preserves inner product \(\langle \cdot, \cdot \rangle\) is linear. Also, Mazur-Ulam theorem states that an onto map \( T : V \to V\) which is an isometry (\( \Vert T(x)-T(y) \Vert = \Vert x-y \Vert \) for all \(x,y \in V\)) and fixes the origin (\(T(0) = 0\)) is linear.

What about an application that preserves the norm (\(\Vert T(x) \Vert = \Vert x \Vert\) for all \(x \in V\))? \(T\) might not be linear as we show with following example:\[
\begin{array}{l|rcll}
T : & V & \longrightarrow & V \\
& x & \longmapsto & x & \text{if } \Vert x \Vert \neq 1\\
& x & \longmapsto & -x & \text{if } \Vert x \Vert = 1\end{array}\]

It is clear that \(T\) preserves the norm. However \(T\) is not linear as soon as \(V\) is not the zero vector space. In that case, consider \(x_0\) such that \(\Vert x_0 \Vert = 1\). We have:\[
\begin{cases}
T(2 x_0) &= 2 x_0 \text{ as } \Vert 2 x_0 \Vert = 2\\
\text{while}\\
T(x_0) + T(x_0) = -x_0 + (-x_0) &= – 2 x_0
\end{cases}\]

Algebra

Non linear map preserving orthogonality

Leave a comment

Let \(V\) be a real vector space endowed with an inner product \(\langle \cdot, \cdot \rangle\).

It is known that a bijective map \( T : V \to V\) that preserves the inner product \(\langle \cdot, \cdot \rangle\) is linear.

That might not be the case if \(T\) is supposed to only preserve orthogonality. Let’s consider for \(V\) the real plane \(\mathbb R^2\) and the map \[
\begin{array}{l|rcll}
T : & \mathbb R^2 & \longrightarrow & \mathbb R^2 \\
& (x,y) & \longmapsto & (x,y) & \text{for } xy \neq 0\\
& (x,0) & \longmapsto & (0,x)\\
& (0,y) & \longmapsto & (y,0) \end{array}\]

The restriction of \(T\) to the plane less the x-axis and the y-axis is the identity and therefore is bijective on this set. Moreover \(T\) is a bijection from the x-axis onto the y-axis, and a bijection from the y-axis onto the x-axis. This proves that \(T\) is bijective on the real plane.

\(T\) preserves the orthogonality on the plane less x-axis and y-axis as it is the identity there. As \(T\) swaps the x-axis and the y-axis, it also preserves orthogonality of the coordinate axes. However, \(T\) is not linear as for non zero \(x \neq y\) we have: \[
\begin{cases}
T[(x,0) + (0,y)] = T[(x,y)] &= (x,y)\\
\text{while}\\
T[(x,0)] + T[(0,y)] = (0,x) + (y,0) &= (y,x)
\end{cases}\]

Algebra

A linear map having all numbers as eigenvalue

Leave a comment

Consider a linear map \(\varphi : E \to E\) where \(E\) is a linear space over the field \(\mathbb C\) of the complex numbers. When \(E\) is a finite dimensional vector space of dimension \(n \ge 1\), the number of eigenvalues is finite. The eigenvalues are the roots of the characteristic polynomial \(\chi_\varphi\) of \(\varphi\). \(\chi_\varphi\) is a complex polynomial of degree \(n \ge 1\). Therefore the set of eigenvalues of \(\varphi\) is non-empty and its cardinal is less than \(n\).

Things are different when \(E\) is an infinite dimensional space.

A linear map having all numbers as eigenvalue

Let’s consider the linear space \(E=\mathcal C^\infty([0,1])\) of smooth complex functions having derivatives of all orders and defined on the segment \([0,1]\). \(E\) is an infinite dimensional space: it contains all the polynomial maps.

On \(E\), we define the linear map \[\begin{array}{l|rcl}
\varphi : & \mathcal C^\infty([0,1]) & \longrightarrow & \mathcal C^\infty([0,1]) \\
& f & \longmapsto & f^\prime \end{array}\]

The set of eigenvalues of \(\varphi\) is all \(\mathbb C\). Indeed, for \(\lambda \in \mathbb C\) the map \(t \mapsto e^{\lambda t}\) is an eigenvector associated to the eigenvalue \(\lambda\).

A linear map having no eigenvalue

On the same linear space \(E=\mathcal C^\infty([0,1])\), we now consider the linear map \[\begin{array}{l|rcl}
\psi : & \mathcal C^\infty([0,1]) & \longrightarrow & \mathcal C^\infty([0,1]) \\
& f & \longmapsto & x f \end{array}\]

Suppose that \(\lambda \in \mathbb C\) is an eigenvalue of \(\psi\) and \(h \in E\) an eigenvector associated to \(\lambda\). By hypothesis, there exists \(x_0 \in [0,1]\) such that \(h(x_0) \neq 0\). Even better, as \(h\) is continuous, \(h\) is non-vanishing on \(J \cap [0,1]\) where \(J\) is an open interval containing \(x_0\). On \(J \cap [0,1]\) we have the equality \[
(\psi(h))(x) = x h(x) = \lambda h(x)\] Hence \(x=\lambda\) for all \(x \in J \cap [0,1]\). A contradiction proving that \(\psi\) has no eigenvalue.

Set Theory

A strictly increasing map that is not one-to-one

Leave a comment

Consider two partially ordered sets \((E,\le)\) and \((F,\le)\) and a strictly increasing map \(f : E \to F\). If the order \((E,\le)\) is total, then \(f\) is one-to-one. Indeed for distinct elements \(x,y \in E\), we have either \(x < y\) or \(y < x\) and consequently \(f(x) < f(y)\) or \(f(y) < f(x)\). Therefore \(f(x)\) and \(f(y)\) are different. This is not true anymore for a partial order \((E,\le)\). We give a counterexample.

Consider a finite set \(E\) having at least two elements and partially ordered by the inclusion. Let \(f\) be the map defined on the powerset \(\wp(E)\) that maps \(A \subseteq E\) to its cardinal \(\vert A \vert \). \(f\) is obviously strictly increasing. However \(f\) is not one-to-one as for distincts elements \(a,b \in E\) we have \[
f(\{a\}) = 1 = f(\{b\})\]

Analysis

Radius of convergence of power series

Leave a comment

We look here at the radius of convergence of the sum and product of power series.

Let’s recall that for a power series \(\displaystyle \sum_{n=0}^\infty a_n x^n\) where \(0\) is not the only convergence point, the radius of convergence is the unique real \(0 < R \le \infty\) such that the series converges whenever \(\vert x \vert < R\) and diverges whenever \(\vert x \vert > R\).

Given two power series with radii of convergence \(R_1\) and \(R_2\), i.e.
\begin{align*}
\displaystyle f_1(x) = \sum_{n=0}^\infty a_n x^n, \ \vert x \vert < R_1 \\ \displaystyle f_2(x) = \sum_{n=0}^\infty b_n x^n, \ \vert x \vert < R_2 \end{align*} The sum of the power series \begin{align*} \displaystyle f_1(x) + f_2(x) &= \sum_{n=0}^\infty a_n x^n + \sum_{n=0}^\infty b_n x^n \\ &=\sum_{n=0}^\infty (a_n + b_n) x^n \end{align*} and its Cauchy product:
\begin{align*}
\displaystyle f_1(x) \cdot f_2(x) &= \left(\sum_{n=0}^\infty a_n x^n\right) \cdot \left(\sum_{n=0}^\infty b_n x^n \right) \\
&=\sum_{n=0}^\infty \left( \sum_{l=0}^n a_l b_{n-l}\right) x^n
\end{align*}
both have radii of convergence greater than or equal to \(\min \{R_1,R_2\}\).

The radii can indeed be greater than \(\min \{R_1,R_2\}\). Let’s give examples.
Continue reading Radius of convergence of power series →

Topology

Isometric versus affine

Leave a comment

Throughout this article we let \(E\) and \(F\) denote real normed vector spaces. A map \(f : E \rightarrow F\) is an isometry if \(\Vert f(x) – f(y) \Vert = \Vert x – y \Vert\) for all \(x, y \in E\), and \(f\) is affine if \[
f((1-t) a + t b ) = (1-t) f(a) + t f(b) \] for all \(a,b \in E\) and \(t \in [0,1]\). Equivalently, \(f\) is affine if the map \(T : E \rightarrow F\), defined by \(T(x)=f(x)-f(0)\) is linear.

First note that an isometry \(f\) is always one-to-one as \(f(x) = f(y)\) implies \[
0 = \Vert f(x) – f(y) \Vert = \Vert x- y \Vert\] hence \(x=y\).

There are two important cases when every isometry is affine:

  1. \(f\) is bijective (equivalently surjective). This is Mazur-Ulam theorem, which was proven in 1932.
  2. \(F\) is a strictly convex space. Recall that a normed vector space \((S, \Vert \cdot \Vert)\) is strictly convex if and only if for all distinct \(x,y \in S\), \(\Vert x \Vert = \Vert y \Vert =1\) implies \(\Vert \frac{x+y}{2} \Vert <1\). For example, an inner product space is strictly convex. The sequence spaces \(\ell_p\) for \(1 < p < \infty\) are also strictly convex.

Continue reading Isometric versus affine →

Analysis

A trigonometric series that is not a Fourier series (Lebesgue-integration)

Leave a comment

We already provided here an example of a trigonometric series that is not the Fourier series of a Riemann-integrable function (namely the function \(\displaystyle x \mapsto \sum_{n=1}^\infty \frac{\sin nx}{\sqrt n}\)).

Applying an Abel-transformation (like mentioned in the link above), one can see that the function \[f(x)=\sum_{n=2}^\infty \frac{\sin nx}{\ln n}\] is everywhere convergent. We now prove that \(f\) cannot be the Fourier series of a Lebesgue-integrable function. The proof is based on the fact that for a \(2 \pi\)-periodic function \(g\), Lebesgue-integrable on \([0,2 \pi]\), the sum \[\sum_{n=1}^\infty \frac{c_n-c_{-n}}{n}\] is convergent where \((c_n)_{n \in \mathbb Z}\) are the complex Fourier coefficients of \(g\): \[c_n = \frac{1}{2 \pi} \int_0^{2 \pi} g(t)e^{-ikt} \ dt.\] As the series \(\displaystyle \sum_{n=2}^\infty \frac{1}{n \ln n}\) is divergent, we will be able to conclude that the sequence defined by \[\gamma_0=\gamma_1=\gamma_{-1} = 0, \, \gamma_n=- \gamma_{-n} = \frac{1}{\ln n} \ (n \ge 2)\] cannot be the Fourier coefficients of a Lebesgue-integrable function, hence that \(f\) is not the Fourier series of any Lebesgue-integrable function. Continue reading A trigonometric series that is not a Fourier series (Lebesgue-integration) →

Analysis

A trigonometric series that is not a Fourier series (Riemann-integration)

1 Comment

We’re looking here at convergent trigonometric series like \[f(x) = a_0 + \sum_{k=1}^\infty (a_n \cos nx + b_n \sin nx)\] which are convergent but are not Fourier series. Which means that the terms \(a_n\) and \(b_n\) cannot be written\[
\begin{array}{ll}
a_n = \frac{1}{\pi} \int_0^{2 \pi} g(t) \cos nt \, dt & (n= 0, 1, \dots) \\
b_n = \frac{1}{\pi} \int_0^{2 \pi} g(t) \sin nt \, dt & (n= 1, 2, \dots)
\end{array}\] where \(g\) is any integrable function.

This raises the question of the type of integral used. We cover here an example based on Riemann integral. I’ll cover a Lebesgue integral example later on.

We prove here that the function \[
f(x)= \sum_{n=1}^\infty \frac{\sin nx}{\sqrt{n}}\] is a convergent trigonometric series but is not a Fourier series. Continue reading A trigonometric series that is not a Fourier series (Riemann-integration) →

Analysis

Counterexamples around Dini’s theorem

Leave a comment

In this article we look at counterexamples around Dini’s theorem. Let’s recall:

Dini’s theorem: If \(K\) is a compact topological space, and \((f_n)_{n \in \mathbb N}\) is a monotonically decreasing sequence (meaning \(f_{n+1}(x) \le f_n(x)\) for all \(n \in \mathbb N\) and \(x \in K\)) of continuous real-valued functions on \(K\) which converges pointwise to a continuous function \(f\), then the convergence is uniform.

We look at what happens to the conclusion if we drop some of the hypothesis.

Cases if \(K\) is not compact

We take \(K=(0,1)\), which is not closed equipped with the common distance. The sequence \(f_n(x)=x^n\) of continuous functions decreases pointwise to the always vanishing function. But the convergence is not uniform because for all \(n \in \mathbb N\) \[\sup\limits_{x \in (0,1)} x^n = 1\]

The set \(K=\mathbb R\) is closed but unbounded, hence also not compact. The sequence defined by \[f_n(x)=\begin{cases}
0 & \text{for } x < n\\ \frac{x-n}{n} & \text{for } n \le x < 2n\\ 1 & \text{for } x \ge 2n \end{cases}\] is continuous and monotonically decreasing. It converges to \(0\). However, the convergence is not uniform as for all \(n \in \mathbb N\): \(\sup\{f_n(x) : x \in \mathbb R\} =1\). Continue reading Counterexamples around Dini’s theorem →