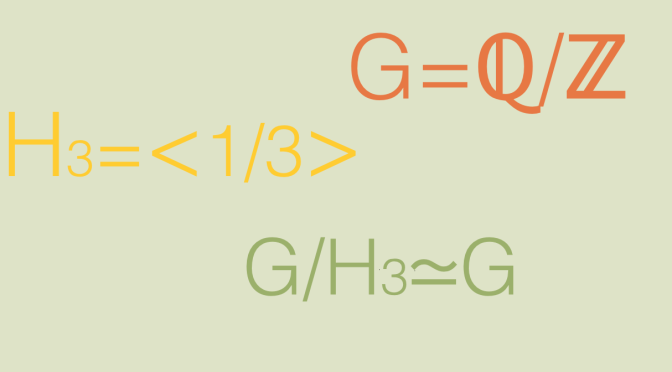The basic question that we raise here is the following one: given a group \(G\) and a proper subgroup \(H\) (i.e. \(H \notin \{\{1\},G\}\), can \(G/H\) be isomorphic to \(G\)? A group \(G\) is said to be hopfian (after Heinz Hopf) if it is not isomorphic with a proper quotient group.

All finite groups are hopfian as \(|G/H| = |G| \div |H|\). Also, all simple groups are hopfian as a simple group doesn’t have proper subgroups.

So we need to turn ourselves to infinite groups to uncover non hopfian groups. Continue reading A (not finitely generated) group isomorphic to a proper quotient group →