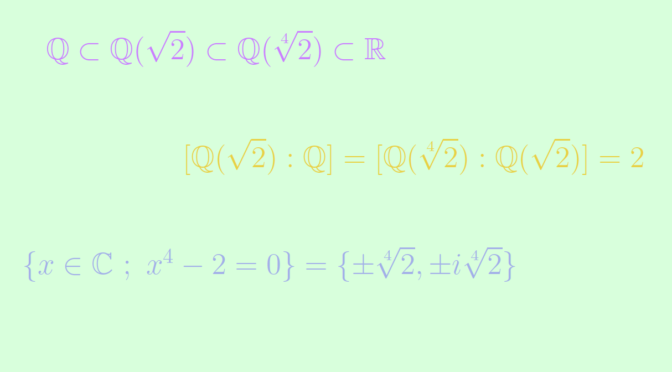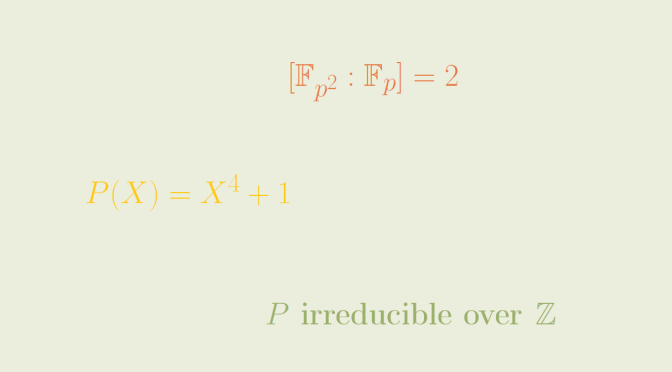An algebraic field extension $K \subset L$ is said to be normal if every irreducible polynomial, either has no root in $L$ or splits into linear factors in $L$.

One can prove that if $L$ is a normal extension of $K$ and if $E$ is an intermediate extension (i.e., $K \subset E \subset L$), then $L$ is a normal extension of $E$.

However a normal extension of a normal extension may not be normal and the extensions $\mathbb Q \subset \mathbb Q(\sqrt{2}) \subset \mathbb Q(\sqrt[4]{2})$ provide a counterexample. Let’s prove it.

As a short lemma, we prove that a quadratic extension $k \subset K$ , i.e. an extension of degree two is normal. Suppose that $P$ is an irreducible polynomial of $k[x]$ with a root $a \in K$. If $a \in k$ then the degree of $P$ is equal to $1$ and we’re done. Otherwise $(1, a)$ is a basis of $K$ over $k$ and there exist $\lambda, \mu \in k$ such that $a^2 = \lambda a +\mu$. As $a \notin k$, $Q(x)= x^2 – \lambda x -\mu$ is the minimal polynomial of $a$ over $k$. As $P$ is supposed to be irreducible, we get $Q = P$. And we can conclude as $$Q(x) = (x-a)(x- \lambda +a).$$

The entensions $\mathbb Q \subset \mathbb Q(\sqrt{2})$ and $\mathbb Q(\sqrt{2}) \subset \mathbb Q(\sqrt[4]{2})$ are quadratic, hence normal according to previous lemma and $\sqrt[4]{2}$ is a root of the polynomial $P(x)= x^4-2$ of $\mathbb Q[x]$. According to Eisenstein’s criterion $P$ is irreducible over $\mathbb Q$. However $\mathbb Q(\sqrt[4]{2}) \subset \mathbb R$ while the roots of $P$ are $\pm \sqrt[4]{2}, \pm i \sqrt[4]{2}$ and therefore not all real. We can conclude that $\mathbb Q \subset \mathbb Q(\sqrt[4]{2})$ is not normal.

Let’s describe an example of a field $K$ which is of degree $2$ over two distinct subfields $M$ and $N$ respectively, but not algebraic over $M \cap N$.

Let $K=F(x)$ be the rational function field over a field $F$ of characteristic $0$, $M=F(x^2)$ and $N=F(x^2+x)$. I claim that those fields provide the example we’re looking for.

$K$ is of degree $2$ over $M$ and $N$

The polynomial $\mu_M(t)=t^2-x^2$ belongs to $M[t]$ and $x \in K$ is a root of $\mu_M$. Also, $\mu_M$ is irreducible over $M=F(x^2)$. If that wasn’t the case, $\mu_M$ would have a root in $F(x^2)$ and there would exist two polynomials $p,q \in F[t]$ such that $$p^2(x^2) = x^2 q^2(x^2)$$ which cannot be, as can be seen considering the degrees of the polynomials of left and right hand sides. This proves that $[K:M]=2$. Considering the polynomial $\mu_N(t)=t^2-t-(x^2+x)$, one can prove that we also have $[K:N]=2$.

We have $M \cap N=F$

The mapping $\sigma_M : x \mapsto -x$ extends uniquely to an $F$-automorphism of $K$ and the elements of $M$ are fixed under $\sigma_M$. Similarly, the mapping $\sigma_N : x \mapsto -x-1$ extends uniquely to an $F$-automorphism of $K$ and the elements of $N$ are fixed under $\sigma_N$. Also $$(\sigma_N\circ\sigma_M)(x)=\sigma_N(\sigma_M(x))=\sigma_N(-x)=-(-x-1)=x+1.$$ An element $z=p(x)/q(x) \in M \cap N$ where $p(x),q(x)$ are coprime polynomials of $K=F(x)$ is fixed under $\sigma_M \circ \sigma_N$. Therefore following equality holds $$\frac{p(x)}{q(x)}=z=(\sigma_2\circ\sigma_1)(z)=\frac{p(x+1)}{q(x+1)},$$ which is equivalent to $$p(x)q(x+1)=p(x+1)q(x).$$ By induction, we get for $n \in \mathbb Z$ $$p(x)q(x+n)=p(x+n)q(x).$$ Assume $p(x)$ is not a constant polynomial. Then it has a root $\alpha$ in some finite extension $E$ of $F$. As $p(x),q(x)$ are coprime polynomials, $q(\alpha) \neq 0$. Consequently $p(\alpha+n)=0$ for all $n \in \mathbb Z$ and the elements $\alpha +n$ are all distinct as the characteristic of $F$ is supposed to be non zero. This implies that $p(x)$ is the zero polynomial, in contradiction with our assumption. Therefore $p(x)$ is a constant polynomial and $q(x)$ also according to a similar proof. Hence $z$ is constant as was supposed to be proven.

Finally, $K=F(x)$ is not algebraic over $F=M \cap N$ as $(1,x, x^2, \dots, x^n, \dots)$ is independent over the field $F$ which concludes our claims on $K, M$ and $N$.

Let’s consider $K/k$ a finite field extension of degree $n$. The following theorem holds.

Theorem: the following conditions are equivalent:

1. The extension contains a primitive element.
2. The number of intermediate fields between $k$ and $K$ is finite.

Our aim here is to describe a finite field extension having infinitely many subfields. Considering the theorem above, we have to look at an extension without a primitive element.

The extension $\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)$ is finite

For $p$ prime, $\mathbb F_p$ denotes the finite field with $p$ elements. $\mathbb F_p(X,Y)$ is the algebraic fraction field of two variables over the field $\mathbb F_p$. $\mathbb F_p(X^p,Y^p)$ is the subfield of $\mathbb F_p(X,Y)$ generated by the elements $X^p,Y^p$. Continue reading A finite extension that contains infinitely many subfields →

We give here an example of a division ring which is not commutative. According to Wedderburn theorem every finite division ring is commutative. So we must turn to infinite division rings to find a non-commutative one, i.e. a skew field.

Let’s introduce the skew field of the Hamilton’s quaternions $$\mathbb H = \left\{\begin{pmatrix} u & -\overline{v} \\ v & \overline{u} \end{pmatrix} \ | \ u,v \in \mathbb C\right\}$$ Continue reading The skew field of Hamilton’s quaternions →