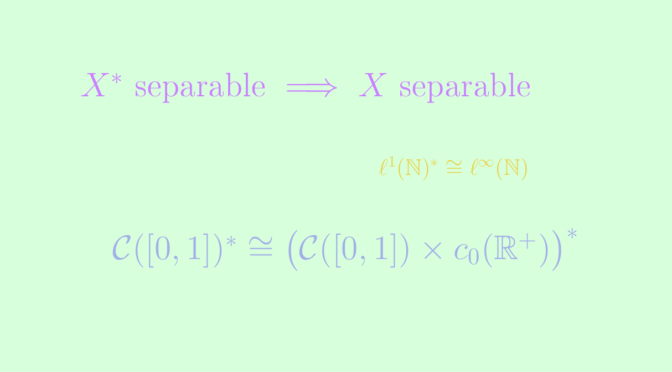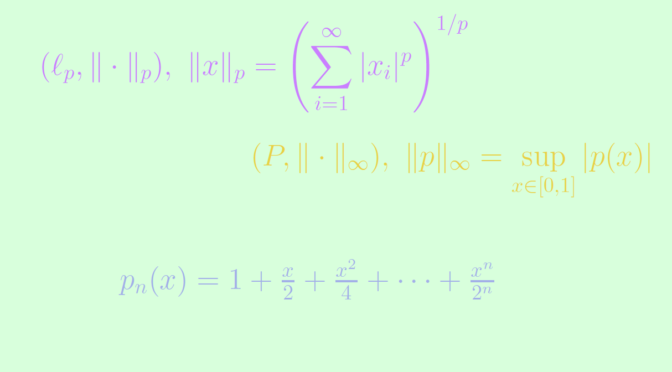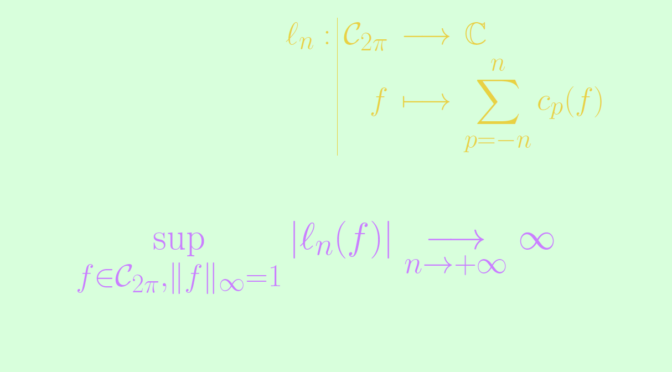Tag Archives: banach-spaces

Topology

Separability of a vector space and its dual

Leave a comment

Recall that a topological space is considered separable when it contains a countable dense set. The following theorem establishes a significant connection between separability and dual spaces:

Theorem: If the dual \(X^*\) of a normed vector space \(X\) is separable, then so is the space \(X\) itself.

Proof outline: let \({f_n}\) be a countable dense set in \(X^*\) unit sphere \(S_*\). For any \(n \in \mathbb{N}\) one can find \(x_n\) in \(X\) unit ball such that \(f_n(x_n) \ge \frac{1}{2}\). We claim that the countable set \(F = \mathrm{Span}_{\mathbb{Q}}(x_0,x_1,…)\) is dense in \(X\). If not, we would find \(x \in X \setminus \overline{F}\) and according to the Hahn-Banach theorem, there would exist a linear functional \(f \in X^*\) such that \(f_{\overline{F}} = 0\) and \(\Vert f \Vert=1\). But then for all \(n \in \mathbb{N}\), \(\Vert f_n-f \Vert \ge \vert f_n(x_n)-f(x_n)\vert = \vert f_n(x_n) \vert \ge \frac{1}{2}\). A contradiction since \({f_n}\) is supposed to be dense in \(S_*\).

We prove that the converse is not true, i.e., a dual space can be separable, while the space itself may not be.

Introducing some normed vector spaces

Given a closed interval \(K \subset \mathbb{R}\) and a set \(A \subset \mathbb{R}\), we define the \(4\) following spaces. The first three are endowed with the supremum norm and the last with the \(\ell^1\) norm.

  • \(\mathcal{C}(K,\mathbb{R})\), the space of continuous functions from \(K\) to \(\mathbb{R}\), is separable as the polynomial functions with coefficients in \(\mathbb{Q}\) are dense and countable.
  • \(\ell^{\infty}(A, \mathbb{R})\) is the space of real bounded functions defined on \(A\) with countable support.
  • \(c_0(A, \mathbb{R}) \subset \ell^{\infty}(A, \mathbb{R})\) is the subspace of elements of \(\ell^{\infty}(A)\) going to \(0\) at \(\infty\).
  • \(\ell^1(A, \mathbb{R})\) is the space of summable functions on \(A\): \(u \in \mathbb{R}^{A}\) is in \(\ell^1(A, \mathbb{R})\) iff \(\sum \limits_{a \in A} |u_x| < +\infty\).

We find the usual sequence spaces when \(A = \mathbb{N}\). It should be noted that \(c_0(A, \mathbb{R})\) and \(\ell^1(A, \mathbb{R})\) are separable iff \(A\) is countable (otherwise the subset \(\big\{x \mapsto 1_{\{a\}}(x),\ a \in A \big\}\) is uncountable, and discrete), and that \(\ell^{\infty}(A, \mathbb{R})\) is separable iff \(A\) is finite (otherwise the subset \(\{0,1\}^A\) is uncountable, and discrete).

Continue reading Separability of a vector space and its dual →
Topology

A non complete normed vector space

Leave a comment

Consider a real normed vector space \(V\). \(V\) is called complete if every Cauchy sequence in \(V\) converges in \(V\). A complete normed vector space is also called a Banach space.

A finite dimensional vector space is complete. This is a consequence of a theorem stating that all norms on finite dimensional vector spaces are equivalent.

There are many examples of Banach spaces with infinite dimension like \((\ell_p, \Vert \cdot \Vert_p)\) the space of real sequences endowed with the norm \(\displaystyle \Vert x \Vert_p = \left( \sum_{i=1}^\infty \vert x_i \vert^p \right)^{1/p}\) for \(p \ge 1\), the space \((C(X), \Vert \cdot \Vert)\) of real continuous functions on a compact Hausdorff space \(X\) endowed with the norm \(\displaystyle \Vert f \Vert = \sup\limits_{x \in X} \vert f(x) \vert\) or the Lebesgue space \((L^1(\mathbb R), \Vert \cdot \Vert_1)\) of Lebesgue real integrable functions endowed with the norm \(\displaystyle \Vert f \Vert = \int_{\mathbb R} \vert f(x) \vert \ dx\).

Let’s give an example of a non complete normed vector space. Let \((P, \Vert \cdot \Vert_\infty)\) be the normed vector space of real polynomials endowed with the norm \(\displaystyle \Vert p \Vert_\infty = \sup\limits_{x \in [0,1]} \vert p(x) \vert\). Consider the sequence of polynomials \((p_n)\) defined by
\[p_n(x) = 1 + \frac{x}{2} + \frac{x^2}{4} + \cdots + \frac{x^n}{2^n} = \sum_{k=0}^{n} \frac{x^k}{2^k}.\] For \(m < n \) and \(x \in [0,1]\), we have \[\vert p_n(x) - p_m(x) \vert = \left\vert \sum_{i=m+1}^n \frac{x^i}{2^i} \right\vert \le \sum_{i=m+1}^n \frac{1}{2^i} \le \frac{1}{2^m}\] which proves that \((p_n)\) is a Cauchy sequence. Also for \(x \in [0,1]\) \[ \lim\limits_{n \to \infty} p_n(x) = p(x) \text{ where } p(x) = \frac{1}{1 - \frac{x}{2}}.\] As uniform converge implies pointwise convergence, if \((p_n)\) was convergent in \(P\), it would be towards \(p\). But \(p\) is not a polynomial function as none of its \(n\)th-derivative always vanishes. Hence \((p_n)\) is a Cauchy sequence that doesn't converge in \((P, \Vert \cdot \Vert_\infty)\), proving as desired that this normed vector space is not complete. More generally, a normed vector space with countable dimension is never complete. This can be proven using Baire category theorem which states that a non-empty complete metric space is not the countable union of nowhere-dense closed sets.

Analysis

Existence of a continuous function with divergent Fourier series

1 Comment

In that article, I provided an example of a continuous function with divergent Fourier series. We prove here the existence of such a function using Banach-Steinhaus theorem, also called uniform boundedness principle.

Theorem (Uniform Boundedness Theorem) Let \((X, \Vert \cdot \Vert_X)\) be a Banach space and \((Y, \Vert \cdot \Vert_Y)\) be a normed vector space. Suppose that \(F\) is a set of continuous linear operators from \(X\) to \(Y\). If for all \(x \in X\) one has \[
\sup\limits_{T \in F} \Vert T(x) \Vert_Y \lt \infty\] then \[
\sup\limits_{T \in F, \ \Vert x \Vert = 1} \Vert T(x) \Vert_Y \lt \infty\]

Let’s take for \(X\) the vector space \(\mathcal C_{2 \pi}\) of continuous functions from \(\mathbb R\) to \(\mathbb C\) which are periodic with period \(2 \pi\) endowed with the norm \(\Vert f \Vert_\infty = \sup\limits_{- \pi \le t \le \pi} \vert f(t) \vert\). \((\mathcal C_{2 \pi}, \Vert \cdot \Vert_\infty)\) is a Banach space. For the vector space \(Y\), we take the complex numbers \(\mathbb C\) endowed with the modulus.

For \(n \in \mathbb N\), the map \[
\begin{array}{l|rcl}
\ell_n : & \mathcal C_{2 \pi} & \longrightarrow & \mathbb C \\
& f & \longmapsto & \displaystyle \sum_{p=-n}^n c_p(f) \end{array}\] is a linear operator, where for \(p \in \mathbb Z\), \(c_p(f)\) denotes the complex Fourier coefficient \[
c_p(f) = \frac{1}{2 \pi} \int_{- \pi}^{\pi} f(t) e^{-i p t} \ dt\]

We now prove that
\begin{align*}
\Lambda_n &= \sup\limits_{f \in \mathcal C_{2 \pi}, \Vert f \Vert_\infty=1} \vert \ell_n(f) \vert\\
&= \frac{1}{2 \pi} \int_{- \pi}^{\pi} \left\vert \frac{\sin (2n+1)\frac{t}{2}}{\sin \frac{t}{2}} \right\vert \ dt = \frac{1}{2 \pi} \int_{- \pi}^{\pi} \left\vert h_n(t) \right\vert \ dt,
\end{align*} where one can notice that the function \[
\begin{array}{l|rcll}
h_n : & [- \pi, \pi] & \longrightarrow & \mathbb C \\
& t & \longmapsto & \frac{\sin (2n+1)\frac{t}{2}}{\sin \frac{t}{2}} &\text{for } t \neq 0\\
& 0 & \longmapsto & 2n+1
\end{array}\] is continuous.
Continue reading Existence of a continuous function with divergent Fourier series →

Topology

Counterexamples around Banach-Steinhaus theorem

Leave a comment

In this article we look at what happens to Banach-Steinhaus theorem when the completness hypothesis is not fulfilled. One form of Banach-Steinhaus theorem is the following one.

Banach-Steinhaus Theorem Let \(T_n : E \to F\) be a sequence of continuous linear maps from a Banach space \(E\) to a normed space \(F\). If for all \(x \in E\) the sequence \(T_n x\) is convergent to \(Tx\), then \(T\) is a continuous linear map.

A sequence of continuous linear maps converging to an unbounded linear map

Let \(c_{00}\) be the vector space of real sequences \(x=(x_n)\) eventually vanishing, equipped with the norm \[\Vert x \Vert = \sup_{n \in \mathbb N} \vert x_n \vert\] For \(n \in \mathbb N\), \(T_n : E \to E\) denotes the linear map defined by \[T_n x = (x_1,2 x_2, \dots, n x_n,0,0, \dots).\] \(T_n\) is continuous as for \(\Vert x \Vert \le 1\), we have
\begin{align*}
\Vert T_n x \Vert &= \Vert (x_1,2 x_2, \dots, n x_n,0,0, \dots) \Vert\\
& = \sup_{1 \le k \le n} \vert k x_k \vert \le n \Vert x \Vert \le n
\end{align*} Continue reading Counterexamples around Banach-Steinhaus theorem →

Topology

Counterexamples to Banach fixed-point theorem

Leave a comment

Let \((X,d)\) be a metric space. Then a map \(T : X \to X\) is called a contraction map if it exists \(0 \le k < 1\) such that \[d(T(x),T(y)) \le k d(x,y)\] for all \(x,y \in X\). According to Banach fixed-point theorem, if \((X,d)\) is a complete metric space and \(T\) a contraction map, then \(T\) admits a fixed-point \(x^* \in X\), i.e. \(T(x^*)=x^*\).

We look here at counterexamples to the Banach fixed-point theorem when some hypothesis are not fulfilled.

First, let’s consider \[\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x+1 \end{array}\] For all \(x,y \in \mathbb R\) we have \(\vert f(x)-f(y) \vert = \vert x- y \vert\). \(f\) is not a contraction, but an isometry. Obviously, \(f\) has no fixed-point.

We now prove that a map satisfying \[d(g(x),g(y)) < d(x,y)\] might also not have a fixed-point. A counterexample is the following map \[\begin{array}{l|rcl} g : & [0,+\infty) & \longrightarrow & [0,+\infty) \\ & x & \longmapsto & \sqrt{1+x^2} \end{array}\] Since \[g^\prime(\xi) = \frac{\xi}{\sqrt{1+\xi^2}} < 1 \text{ for all } \xi \in [0, +\infty),\] by the mean value theorem \[\vert g(x) - g(y)| = \vert g^\prime(\xi)\vert |x-y| < |x-y| \text{ for all } x, y \in [0, +\infty).\] However \(g\) has no fixed-point. Finally, let's have a look to a space \((X,d)\) which is not complete. We take \(a,b \in \mathbb R\) with \(0 < a < 1\) and for \((X,d)\) the space \(X = \mathbb R \setminus \{\frac{b}{1-a}\}\) equipped with absolute value distance. \(X\) is not complete. Consider the map \[\begin{array}{l|rcl} h : & X & \longrightarrow & X \\ & x & \longmapsto & ax + b \end{array}\] \(h\) is well defined as for \(x \neq \frac{b}{1-a}\), \(h(x) \neq \frac{b}{1-a}\). \(h\) is a contraction map as for \(x,y \in \mathbb R\) \[\vert h(x)-h(y) \vert = a \vert x - y \vert \] However, \(h\) doesn't have a fixed-point in \(X\) as \(\frac{b}{1-a}\) is the only real for which \(h(x)=x\).

Topology

Counterexample around Arzela-Ascoli theorem

Leave a comment

Let’s recall Arzelà–Ascoli theorem:

Suppose that \(F\) is a Banach space and \(E\) a compact metric space. A subset \(\mathcal{H}\) of the Banach space \(\mathcal{C}_F(E)\) is relatively compact in the topology induced by the uniform norm if and only if it is equicontinuous and and for all \(x \in E\), the set \(\mathcal{H}(x)=\{f(x) \ | \ f \in \mathcal{H}\}\) is relatively compact.

We look here at what happens if we drop the requirement on space \(E\) to be compact and provide a counterexample where the conclusion of Arzelà–Ascoli theorem doesn’t hold anymore.

We take for \(E\) the real interval \([0,+\infty)\) and for all \(n \in \mathbb{N} \setminus \{0\}\) the real function
\[f_n(t)= \sin \sqrt{t+4 n^2 \pi^2}\] We prove that \((f_n)\) is equicontinuous, converges pointwise to \(0\) but is not relatively compact.

According to the mean value theorem, for all \(x,y \in \mathbb{R}\)
\[\vert \sin x – \sin y \vert \le \vert x – y \vert\] Hence for \(n \ge 1\) and \(x,y \in [0,+\infty)\)
\begin{align*}
\vert f_n(x)-f_n(y) \vert &\le \vert \sqrt{x+4 n^2 \pi^2} -\sqrt{y+4 n^2 \pi^2} \vert \\
&= \frac{\vert x – y \vert}{\sqrt{x+4 n^2 \pi^2} +\sqrt{y+4 n^2 \pi^2}} \\
&\le \frac{\vert x – y \vert}{4 \pi}
\end{align*} using multiplication by the conjugate.

Which enables to prove that \((f_n)\) is equicontinuous.

We also have for \(n \ge 1\) and \(x \in [0,+\infty)\)
\begin{align*}
\vert f_n(x) \vert &= \vert f_n(x) – f_n(0) \vert \le \vert \sqrt{x+4 n^2 \pi^2} -\sqrt{4 n^2 \pi^2} \vert \\
&= \frac{\vert x \vert}{\sqrt{x+4 n^2 \pi^2} +\sqrt{4 n^2 \pi^2}} \\
&\le \frac{\vert x \vert}{4 n \pi}
\end{align*}

Hence \((f_n)\) converges pointwise to \(0\) and for \(t \in [0,+\infty), \mathcal{H}(t)=\{f_n(t) \ | \ n \in \mathbb{N} \setminus \{0\}\}\) is relatively compact

Finally we prove that \(\mathcal{H}=\{f_n \ | \ n \in \mathbb{N} \setminus \{0\}\}\) is not relatively compact. While \((f_n)\) converges pointwise to \(0\), \((f_n)\) does not converge uniformly to \(f=0\). Actually for \(n \ge 1\) and \(t_n=\frac{\pi^2}{4} + 2n \pi^2\) we have
\[f_n(t_n)= \sin \sqrt{\frac{\pi^2}{4} + 2n \pi^2 +4 n^2 \pi^2}=\sin \sqrt{\left(\frac{\pi}{2} + 2 n \pi\right)^2}=1\] Consequently for all \(n \ge 1\) \(\Vert f_n – f \Vert_\infty \ge 1\). If \(\mathcal{H}\) was relatively compact, \((f_n)\) would have a convergent subsequence with \(f=0\) for limit. And that cannot be as for all \(n \ge 1\) \(\Vert f_n – f \Vert_\infty \ge 1\).

Topology

Distance between a point and a hyperplane not reached

Leave a comment

Let’s investigate the following question: “Is the distance between a point and a hyperplane always reached?”

In order to provide answers to the question, we consider a normed vector space \((E, \Vert \cdot \Vert)\) and a hyperplane \(H\) of \(E\). \(H\) is the kernel of a non-zero linear form. Namely, \(H=\{x \in E \text{ | } u(x)=0\}\).

The case of finite dimensional vector spaces

When \(E\) is of finite dimension, the distance \(d(a,H)=\inf\{\Vert h-a \Vert \text{ | } h \in H\}\) between any point \(a \in E\) and a hyperplane \(H\) is reached at a point \(b \in H\). The proof is rather simple. Consider a point \(c \in H\). The set \(S = \{h \in H \text{ | } \Vert a- h \Vert \le \Vert a-c \Vert \}\) is bounded as for \(h \in S\) we have \(\Vert h \Vert \le \Vert a-c \Vert + \Vert a \Vert\). \(S\) is equal to \(D \cap H\) where \(D\) is the inverse image of the closed real segment \([0,\Vert a-c \Vert]\) by the continuous map \(f: x \mapsto \Vert a- x \Vert\). Therefore \(D\) is closed. \(H\) is also closed as any linear subspace of a finite dimensional vector space. \(S\) being the intersection of two closed subsets of \(E\) is also closed. Hence \(S\) is compact and the restriction of \(f\) to \(S\) reaches its infimum at some point \(b \in S \subset H\) where \(d(a,H)=\Vert a-b \Vert\). Continue reading Distance between a point and a hyperplane not reached →

Analysis

A solution of a differential equation not exploding in finite time

2 Comments


In this post, I mention that Peano existence theorem is valid for finite dimensional vector spaces, but not for Banach spaces of infinite dimension. I highlight here a second property of ordinary differential equations which is valid for finite dimensional vector spaces but not for infinite dimensional Banach spaces. Continue reading A solution of a differential equation not exploding in finite time →

Topology

An empty intersection of nested closed convex subsets in a Banach space

Leave a comment

We consider a decreasing sequence \((C_n)_{n \in \mathbb{N}}\) of non empty closed convex subsets of a Banach space \(E\).

If the convex subsets are closed balls, their intersection is not empty. To see this let \(x_n\) be the center and \(r_n > 0\) the radius of the ball \(C_n\). For \(0 \leq n < m\) we have \(\Vert x_m-x_n\Vert \leq r_n – r_m\) which proves that \((x_n)_{n \in \mathbb{N}}\) is a Cauchy sequence. As the space \(E\) is Banach, \((x_n)_{n \in \mathbb{N}}\) converges to a limit \(x\) and \(x \in \bigcap_{n=0}^{+\infty} C_n\). Continue reading An empty intersection of nested closed convex subsets in a Banach space →