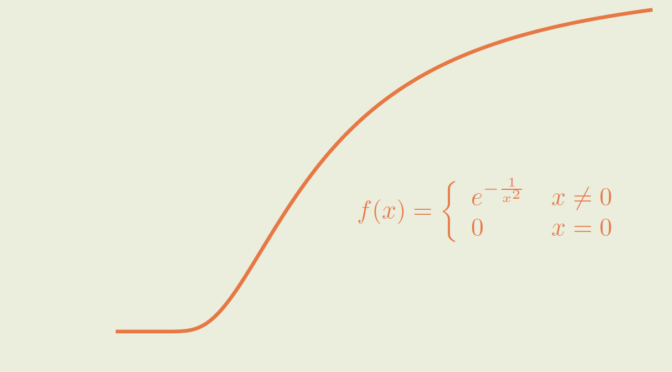Tag Archives: analysis

Analysis

A positive smooth function with all derivatives vanishing at zero

Leave a comment

Let’s consider the set \(\mathcal C^\infty(\mathbb R)\) of real smooth functions, i.e. functions that have derivatives of all orders on \(\mathbb R\).

Does a positive function \(f \in \mathcal C^\infty(\mathbb R)\) with all derivatives vanishing at zero exists?

Such a map \(f\) cannot be expandable in power series around zero, as it would vanish in a neighborhood of zero. However, the answer to our question is positive and we’ll prove that \[
f(x) = \left\{\begin{array}{lll}
e^{-\frac{1}{x^2}} &\text{if} &x \neq 0\\
0 &\text{if} &x = 0 \end{array}\right. \] provides an example.

\(f\) is well defined and positive for \(x \neq 0\). As \(\lim\limits_{x \to 0} -\frac{1}{x^2} = -\infty\), we get \(\lim\limits_{x \to 0} f(x) = 0\) proving that \(f\) is continuous on \(\mathbb R\). Let’s prove by induction that for \(x \neq 0\) and \(n \in \mathbb N\), \(f^{(n)}(x)\) can be written as \[
f^{(n)}(x) = \frac{P_n(x)}{x^{3n}}e^{-\frac{1}{x^2}}\] where \(P_n\) is a polynomial function. The statement is satisfied for \(n = 1\) as \(f^\prime(x) = \frac{2}{x^3}e^{-\frac{1}{x^2}}\). Suppose that the statement is true for \(n\) then \[
f^{(n+1)}(x)=\left[\frac{P_n^\prime(x)}{x^{3n}} – \frac{3n P_n(x)}{x^{3n+1}}+\frac{2 P_n(x)}{x^{3n+3}}\right] e^{-\frac{1}{x^2}}\] hence the statement is also true for \(n+1\) by taking \(P_{n+1}(x)=
x^3 P_n^\prime(x) – 3n x^2 P_n(x) + 2 P_n(x)\). Which concludes our induction proof.

Finally, we have to prove that for all \(n \in \mathbb N\), \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\). For that, we use the power expansion of the exponential map \(e^x = \sum_{n=0}^\infty \frac{x^n}{n!}\). For \(x \neq 0\), we have \[
\left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} \ge \frac{\vert x \vert^{3n}}{(2n)! \vert x \vert ^{4n}} = \frac{1}{(2n)! \vert x \vert^n}\] Therefore \(\lim\limits_{x \to 0} \left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} = \infty\) and \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\) as \(f^{(n)}(x) = \frac{P_n(x)}{x^{3n} e^{\frac{1}{x^2}}}\) with \(P_n\) a polynomial function.

Analysis

Counterexample around infinite products

Leave a comment

Let’s recall two theorems about infinite products \(\prod \ (1+a_n)\). The first one deals with nonnegative terms \(a_n\).

THEOREM 1 An infinite product \(\prod \ (1+a_n)\) with nonnegative terms \(a_n\) converges if and only if the series \(\sum a_n\) converges.

The second is related to infinite products with complex terms.

THEOREM 2 The absolute convergence of the series \(\sum a_n\) implies the convergence of the infinite product \(\prod \ (1+a_n)\). Moreover \(\prod \ (1+a_n)\) is not zero providing \(a_n \neq -1\) for all \(n \in \mathbb N\).

The converse of Theorem 2 is not true as shown by following counterexample.

We consider \(a_n=(-1)^n/(n+1)\). For \(N \in \mathbb N\) we have:
\[\prod_{n=1}^N \ (1+a_n) =
\begin{cases}
\frac{1}{2} &\text{ for } N \text{ odd}\\
\frac{1}{2}(1+\frac{1}{N+1}) &\text{ for } N \text{ even}
\end{cases}
\] hence the infinite product \(\prod \ (1+a_n)\) converges (to \(\frac{1}{2}\)) while the series \(\sum \left\vert a_n \right\vert = \sum \frac{1}{n+1}\) diverges (it is the harmonic series with first term omitted).

Analysis

Counterexample around L’Hôpital’s rule

Leave a comment

Let us consider two differentiable functions \(f\) and \(g\) defined in an open interval \((a,b)\), where \(b\) might be \(\infty\). If
\[\lim\limits_{x \to b^-} f(x) = \lim\limits_{x \to b^-} g(x) = \infty\] and if \(g^\prime(x) \neq 0\) in some interval \((c,b)\), then a version of l’Hôpital’s rule states that \(\lim\limits_{x \to b^-} \frac{f^\prime(x)}{g^\prime(x)} = L\) implies \(\lim\limits_{x \to b^-} \frac{f(x)}{g(x)} = L\).

We provide a counterexample when \(g^\prime\) vanishes in all neighborhood of \(b\). The counterexample is due to the Austrian mathematician Otto Stolz.

We take \((0,\infty)\) for the interval \((a,b)\) and \[
\begin{cases}
f(x) &= x + \cos x \sin x\\
g(x) &= e^{\sin x}(x + \cos x \sin x)
\end{cases}\] which derivatives are \[
\begin{cases}
f^\prime(x) &= 2 \cos^2 x\\
g^\prime(x) &= e^{\sin x} \cos x (x + \cos x \sin x + 2 \cos x)
\end{cases}\] We have \[
\lim\limits_{x \to \infty} \frac{f^\prime(x)}{g^\prime(x)} = \lim\limits_{x \to \infty} \frac{2 \cos x}{e^{\sin x} (x + \cos x \sin x + 2 \cos x)} = 0,\] however \[
\frac{f(x)}{g(x)} = \frac{1}{e^{\sin x}}\] doesn’t have any limit at \(\infty\) as it oscillates between \(\frac{1}{e}\) and \(e\).

Analysis

The Schwarz lantern

Leave a comment

Consider a smooth curve defined by a continuous map \(f : [0,1] \to \mathbb R^n\) with \(n \ge 2\) where \(f\) is supposed to have a continuous derivative. One can prove that the curve is rectifiable, its arc length being \[
L = \lim\limits_{n \to \infty} \sum_{i=1}^n \vert f(t_i) – f(t_{i-1}) \vert = \int_0^1 \vert f^\prime (t) \vert \ dt\] with \(t_i = \frac{i}{n}\) for \(0 \le i \le n\).

What can happen when we consider a surface instead of a curve?

Consider a compact, smooth surface (possibly with boundary) embedded in \(\mathbb R^3\). We can approximate it as a polyhedral surface composed of small triangles with all vertices on the initial surface. Will the sum of the areas of the triangles converges to the area of the surface if their size is converging to zero?

The answer is negative and we provide a counterexample named Schwarz lantern. We take a cylinder of radius \(r\) and height \(h\). We approximate the cylinder by \(4nm\) isosceles triangles positioned as in the picture in \(2n\) slices. All triangles have the same base and height given by \[
b = 2r \sin \left(\frac{\pi}{m}\right), \ h = \sqrt{r^2 \left[1-\cos \left(\frac{\pi}{m}\right)\right]^2+\left(\frac{h}{2n}\right)^2}\] Hence the area of the polyhedral surface is \[
\begin{aligned}
S^\prime(m,n) &= 4 m n r \sin \left(\frac{\pi}{m}\right) \sqrt{r^2 \left[1-\cos \left(\frac{\pi}{m}\right)\right]^2+\left(\frac{h}{2n}\right)^2}\\
&= 4 m n r \sin \left(\frac{\pi}{m}\right) \sqrt{4 r^2 \sin^4 \left(\frac{\pi}{2m} \right)+\left(\frac{h}{2n}\right)^2}
\end{aligned}\] From there, let’s have a look to the value of \(S^\prime(m,n)\) as \(m,n \to \infty\).

Continue reading The Schwarz lantern →

Analysis

Counterexamples around Lebesgue’s Dominated Convergence Theorem

Leave a comment

Let’s recall Lebesgue’s Dominated Convergence Theorem. Let \((f_n)\) be a sequence of real-valued measurable functions on a measure space \((X, \Sigma, \mu)\). Suppose that the sequence converges pointwise to a function \(f\) and is dominated by some integrable function \(g\) in the sense that \[
\vert f_n(x) \vert \le g (x)\] for all \(n \in \mathbb N\) and all \(x \in X\).
Then \(f\) is integrable and \[
\lim\limits_{n \to \infty} \int_X f_n(x) \ d \mu = \int_X f(x) \ d \mu\]

Let’s see what can happen if we drop the domination condition.

We consider the space \(\mathbb R\) endowed with Lebesgue measure and for \(E \subseteq \mathbb R\) we denote by \(\chi_E\) the indicator function of \(E\) defined by \[
\chi_E(x)=\begin{cases}
1 \text{ if } x \in E\\
0 \text{ otherwise}\end{cases}\] For \(n \in \mathbb N\), the function \(f_n=\frac{1}{2n}\chi_{(n^2-n,n^2+n)}\) is measurable and we have \[
\int_{\mathbb R} \frac{1}{2n}\chi_{(n^2-n,n^2+n)}(x) \ dx = \int_{n^2-n}^{n^2+n} \frac{1}{2n} \ dx = 1\] The sequence \((f_n)\) converges uniformly (and therefore pointwise) to the always vanishing function as for \(n \in \mathbb N\) we have for all \(x \in \mathbb R\) \(\vert f_n(x) \vert \le \frac{1}{2n}\). Hence the conclusion of Lebesgue’s Dominated Convergence Theorem doesn’t hold for the sequence \((f_n)\).

Let’s verify that the sequence \((f_n)\) is not dominated by some integrable function \(g\). For \(p < q\) integers, we have \[ \begin{aligned} q^2-q-(p^2+p) &= q^2-p^2 -q-p\\ &= (q-p)(q+p) -q -p\\ &\ge (q+p) -q-p=0 \end{aligned}\] Hence for \(p \neq q\) integers the intervals \((p^2-p,p^2+p)\) and \((q^2-q,q^2+q)\) are disjoint. Consequently for all \(x \in \mathbb R\) the sum \(\sum_{n \in \mathbb N} f_n(x)\) amounts to only one term and the function \(\sum_{n \in \mathbb N} f_n\) is well defined. If \(g\) dominates the sequence \((f_n)\), it satisfies \(0 \le \sum_{n \in \mathbb N} f_n \le g\). But \[ \int_{\mathbb R} \sum_{n \in \mathbb N} f_n(x) \ dx = \sum_{n \in \mathbb N} \int_{\mathbb R} f_n(x) \ dx = \sum_{n \in \mathbb N} 1 = \infty\] and \(g\) cannot be integrable. Continue reading Counterexamples around Lebesgue’s Dominated Convergence Theorem →

Analysis

Bounded functions and infimum, supremum

Leave a comment

According to the extreme value theorem, a continuous real-valued function \(f\) in the closed and bounded interval \([a,b]\) must attain a maximum and a minimum, each at least once.

Let’s see what can happen for non-continuous functions. We consider below maps defined on \([0,1]\).

First let’s look at \[
f(x)=\begin{cases}
x &\text{ if } x \in (0,1)\\
1/2 &\text{otherwise}
\end{cases}\] \(f\) is bounded on \([0,1]\), continuous on the interval \((0,1)\) but neither at \(0\) nor at \(1\). The infimum of \(f\) is \(0\), its supremum \(1\), and \(f\) doesn’t attain those values. However, for \(0 < a < b < 1\), \(f\) attains its supremum and infimum on \([a,b]\) as \(f\) is continuous on this interval.

Bounded function that doesn’t attain its infimum and supremum on all \([a,b] \subseteq [0,1]\)

The function \(g\) defined on \([0,1]\) by \[
g(x)=\begin{cases}
0 & \text{ if } x \notin \mathbb Q \text{ or if } x = 0\\
\frac{(-1)^q (q-1)}{q} & \text{ if } x = \frac{p}{q} \neq 0 \text{, with } p, q \text{ relatively prime}
\end{cases}\] is bounded, as for \(x \in \mathbb Q \cap [0,1]\) we have \[
\left\vert g(x) \right\vert < 1.\] Hence \(g\) takes values in the interval \([-1,1]\). We prove that the infimum of \(g\) is \(-1\) and its supremum \(1\) on all intervals \([a,b]\) with \(0 < a < b <1\). Consider \(\varepsilon > 0\) and an odd prime \(q\) such that \[
q > \max(\frac{1}{\varepsilon}, \frac{1}{b-a}).\] This is possible as there are infinitely many prime numbers. By the pigeonhole principle and as \(0 < \frac{1}{q} < b-a\), there exists a natural number \(p\) such that \(\frac{p}{q} \in (a,b)\). We have \[ -1 < g \left(\frac{p}{q} \right) = \frac{(-1)^q (q-1)}{q} = - \frac{q-1}{q} <-1 +\varepsilon\] as \(q\) is supposed to be an odd prime with \(q > \frac{1}{\varepsilon}\). This proves that the infimum of \(g\) is \(-1\). By similar arguments, one can prove that the supremum of \(g\) on \([a,b]\) is \(1\).

Analysis

On limit at infinity of functions and their derivatives

Leave a comment

We consider continuously differentiable real functions defined on \((0,\infty)\) and the limits \[
\lim\limits_{x \to \infty} f(x) \text{ and } \lim\limits_{x \to \infty} f^\prime(x).\]

A map \(f\) such that \(\lim\limits_{x \to \infty} f(x) = \infty\) and \(\lim\limits_{x \to \infty} f^\prime(x) = 0\)

Consider the map \(f : x \mapsto \sqrt{x}\). It is clear that \(\lim\limits_{x \to \infty} f(x) = \infty\). As \(f^\prime(x) = \frac{1}{2 \sqrt{x}}\), we have as announced \(\lim\limits_{x \to \infty} f^\prime(x) = 0\)

A bounded map \(g\) having no limit at infinity such that \(\lim\limits_{x \to \infty} g^\prime(x) = 0\)

One idea is to take an oscillating map whose wavelength is increasing to \(\infty\). Let’s take the map \(g : x \mapsto \cos \sqrt{x}\). \(g\) doesn’t have a limit at \(\infty\) as for \(n \in \mathbb N\), we have \(g(n^2 \pi^2) = \cos n \pi = (-1)^n\). However, the derivative of \(g\) is \[
g^\prime(x) = – \frac{\sin \sqrt{x}}{2 \sqrt{x}},\] and as \(\vert g^\prime(x) \vert \le \frac{1}{2 \sqrt{x}}\) for all \(x \in (0,\infty)\), we have \(\lim\limits_{x \to \infty} g^\prime(x) = 0\).

Analysis

Limit points of real sequences

1 Comment

Let’s start by recalling an important theorem of real analysis:

THEOREM. A necessary and sufficient condition for the convergence of a real sequence is that it is bounded and has a unique limit point.

As a consequence of the theorem, a sequence having a unique limit point is divergent if it is unbounded. An example of such a sequence is the sequence \[
u_n = \frac{n}{2}(1+(-1)^n),\] whose initial values are \[
0, 1, 0, 2, 0, 3, 0, 4, 0, 5, 6, \dots\] \((u_n)\) is an unbounded sequence whose unique limit point is \(0\).

Let’s now look at sequences having more complicated limit points sets.

A sequence whose set of limit points is the set of natural numbers

Consider the sequence \((v_n)\) whose initial terms are \[
1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, \dots\] \((v_n)\) is defined as follows \[
v_n=\begin{cases}
1 &\text{ for } n= 1\\
n – \frac{k(k+1)}{2} &\text{ for } \frac{k(k+1)}{2} \lt n \le \frac{(k+1)(k+2)}{2}
\end{cases}\] \((v_n)\) is well defined as the sequence \((\frac{k(k+1)}{2})_{k \in \mathbb N}\) is strictly increasing with first term equal to \(1\). \((v_n)\) is a sequence of natural numbers. As \(\mathbb N\) is a set of isolated points of \(\mathbb R\), we have \(V \subseteq \mathbb N\), where \(V\) is the set of limit points of \((v_n)\). Conversely, let’s take \(m \in \mathbb N\). For \(k + 1 \ge m\), we have \(\frac{k(k+1)}{2} + m \le \frac{(k+1)(k+2)}{2}\), hence \[
u_{\frac{k(k+1)}{2} + m} = m\] which proves that \(m\) is a limit point of \((v_n)\). Finally the set of limit points of \((v_n)\) is the set of natural numbers.

Continue reading Limit points of real sequences →

Analysis

A power series converging everywhere on its circle of convergence defining a non-continuous function

Leave a comment

Consider a complex power series \(\displaystyle \sum_{k=0}^\infty a_k z^k\) with radius of convergence \(0 \lt R \lt \infty\) and suppose that for every \(w\) with \(\vert w \vert = R\), \(\displaystyle \sum_{k=0}^\infty a_k w^k\) converges.

We provide an example where the power expansion at the origin \[
\displaystyle f(z) = \sum_{k=0}^\infty a_k z^k\] is discontinuous on the closed disk \(\vert z \vert \le R \).

The function \(f\) is constructed as an infinite sum \[
\displaystyle f(z) = \sum_{n=1}^\infty f_n(z)\] with \(f_n(z) = \frac{\delta_n}{a_n-z}\) where \((\delta_n)_{n \in \mathbb N}\) is a sequence of positive real numbers and \((a_n)\) a sequence of complex numbers of modulus larger than one and converging to one. Let \(f_n^{(r)}(z)\) denote the sum of the first \(r\) terms in the power series expansion of \(f_n(z)\) and \(\displaystyle f^{(r)}(z) \equiv \sum_{n=1}^\infty f_n^{(r)}(z)\).

We’ll prove that:

  1. If \(\sum_n \delta_n \lt \infty\) then \(\sum_{n=1}^\infty f_n^{(r)}(z)\) converges and \(f(z) = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(z)\) for \(\vert z \vert \le 1\) and \(z \neq 1\).
  2. If \(a_n=1+i \epsilon_n\) and \(\sum_n \delta_n/\epsilon_n < \infty\) then \(\sum_{n=1}^\infty f_n^{(r)}(1)\) converges and \(f(1) = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(1)\)
  3. If \(\delta_n/\epsilon_n^2 \to \infty\) then \(f(z)\) is unbounded on the disk \(\vert z \vert \le 1\).

First, let’s recall this corollary of Lebesgue’s dominated convergence theorem:

Let \((u_{n,i})_{(n,i) \in \mathbb N \times \mathbb N}\) be a double sequence of complex numbers. Suppose that \(u_{n,i} \to v_i\) for all \(i\) as \(n \to \infty\), and that \(\vert u_{n,i} \vert \le w_i\) for all \(n\) with \(\sum_i w_i < \infty\). Then for all \(n\) the series \(\sum_i u_{n,i}\) is absolutely convergent and \(\lim_n \sum_i u_{n,i} = \sum_i v_i\).
Continue reading A power series converging everywhere on its circle of convergence defining a non-continuous function →

Analysis

A uniformly but not normally convergent function series

Leave a comment

Consider a functions series \(\displaystyle \sum f_n\) of functions defined on a set \(S\) to \(\mathbb R\) or \(\mathbb C\). It is known that if \(\displaystyle \sum f_n\) is normally convergent, then \(\displaystyle \sum f_n\) is uniformly convergent.

The converse is not true and we provide two counterexamples.

Consider first the sequence of functions \((g_n)\) defined on \(\mathbb R\) by:
\[g_n(x) = \begin{cases}
\frac{\sin^2 x}{n} & \text{for } x \in (n \pi, (n+1) \pi)\\
0 & \text{else}
\end{cases}\] The series \(\displaystyle \sum \Vert g_n \Vert_\infty\) diverges as for all \(n \in \mathbb N\), \(\Vert g_n \Vert_\infty = \frac{1}{n}\) and the harmonic series \(\sum \frac{1}{n}\) diverges. However the series \(\displaystyle \sum g_n\) converges uniformly as for \(x \in \mathbb R\) the sum \(\displaystyle \sum g_n(x)\) is having only one term and \[
\vert R_n(x) \vert = \left\vert \sum_{k=n+1}^\infty g_k(x) \right\vert \le \frac{1}{n+1}\]

For our second example, we consider the sequence of functions \((f_n)\) defined on \([0,1]\) by \(f_n(x) = (-1)^n \frac{x^n}{n}\). For \(x \in [0,1]\) \(\displaystyle \sum (-1)^n \frac{x^n}{n}\) is an alternating series whose absolute value of the terms converge to \(0\) monotonically. According to Leibniz test, \(\displaystyle \sum (-1)^n \frac{x^n}{n}\) is well defined and we can apply the classical inequality \[
\displaystyle \left\vert \sum_{k=1}^\infty (-1)^k \frac{x^k}{k} – \sum_{k=1}^m (-1)^k \frac{x^k}{k} \right\vert \le \frac{x^{m+1}}{m+1} \le \frac{1}{m+1}\] for \(m \ge 1\). Which proves that \(\displaystyle \sum (-1)^n \frac{x^n}{n}\) converges uniformly on \([0,1]\).

However the convergence is not normal as \(\sup\limits_{x \in [0,1]} \frac{x^n}{n} = \frac{1}{n}\).