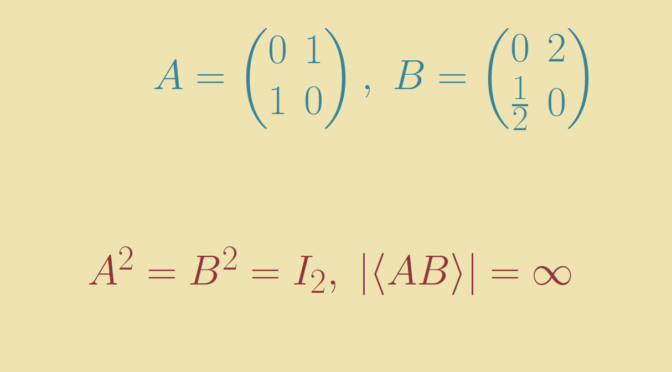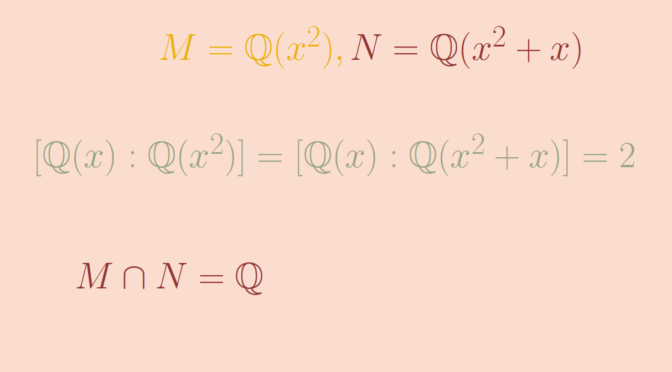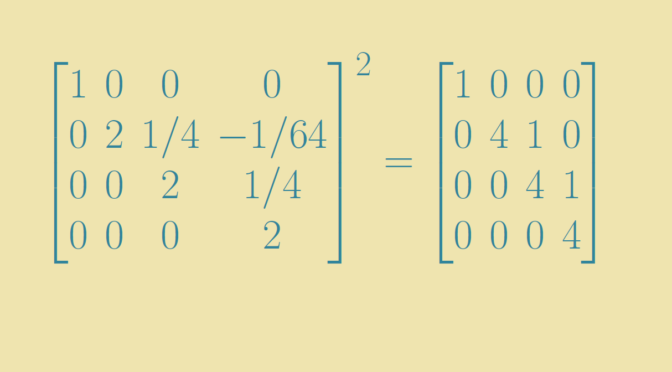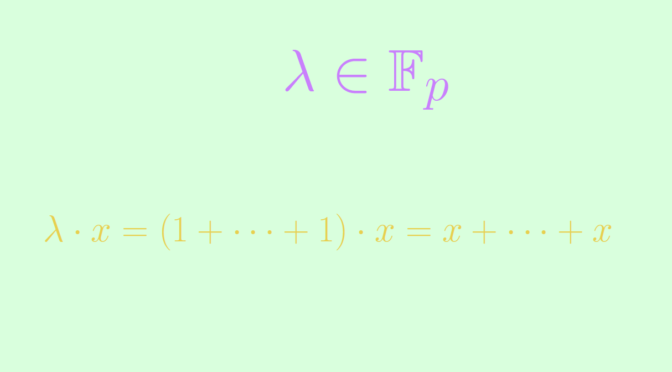Tag Archives: algebra

Algebra

Subset of elements of finite order of a group

Leave a comment

Consider a group \(G\) and have a look at the question: is the subset \(S\) of elements of finite order a subgroup of \(G\)?

The answer is positive when any two elements of \(S\) commute. For the proof, consider \(x,y \in S\) of order \(m,n\) respectively. Then \[
\left(xy\right)^{mn} = x^{mn} y^{mn} = (x^m)^n (y^n)^m = e\] where \(e\) is the identity element. Hence \(xy\) is of finite order (less or equal to \(mn\)) and belong to \(S\).

Example of a non abelian group

In that cas, \(S\) might not be subgroup of \(G\). Let’s take for \(G\) the general linear group over \(\mathbb Q\) (the set of rational numbers) of \(2 \times 2\) invertible matrices named \(\text{GL}_2(\mathbb Q)\). The matrices \[
A = \begin{pmatrix}0&1\\1&0\end{pmatrix},\ B=\begin{pmatrix}0 & 2\\\frac{1}{2}& 0\end{pmatrix}\] are of order \(2\). They don’t commute as \[
AB = \begin{pmatrix}\frac{1}{2}&0\\0&2\end{pmatrix} \neq \begin{pmatrix}2&0\\0&\frac{1}{2}\end{pmatrix}=BA.\] Finally, \(AB\) is of infinite order and therefore doesn’t belong to \(S\) proving that \(S\) is not a subgroup of \(G\).

Algebra

Field not algebraic over an intersection but algebraic over each initial field

Leave a comment

Let’s describe an example of a field \(K\) which is of degree \(2\) over two distinct subfields \(M\) and \(N\) respectively, but not algebraic over \(M \cap N\).

Let \(K=F(x)\) be the rational function field over a field \(F\) of characteristic \(0\), \(M=F(x^2)\) and \(N=F(x^2+x)\). I claim that those fields provide the example we’re looking for.

\(K\) is of degree \(2\) over \(M\) and \(N\)

The polynomial \(\mu_M(t)=t^2-x^2\) belongs to \(M[t]\) and \(x \in K\) is a root of \(\mu_M\). Also, \(\mu_M\) is irreducible over \(M=F(x^2)\). If that wasn’t the case, \(\mu_M\) would have a root in \(F(x^2)\) and there would exist two polynomials \(p,q \in F[t]\) such that \[
p^2(x^2) = x^2 q^2(x^2)\] which cannot be, as can be seen considering the degrees of the polynomials of left and right hand sides. This proves that \([K:M]=2\). Considering the polynomial \(\mu_N(t)=t^2-t-(x^2+x)\), one can prove that we also have \([K:N]=2\).

We have \(M \cap N=F\)

The mapping \(\sigma_M : x \mapsto -x\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(M\) are fixed under \(\sigma_M\). Similarly, the mapping \(\sigma_N : x \mapsto -x-1\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(N\) are fixed under \(\sigma_N\). Also \[
(\sigma_N\circ\sigma_M)(x)=\sigma_N(\sigma_M(x))=\sigma_N(-x)=-(-x-1)=x+1.\] An element \(z=p(x)/q(x) \in M \cap N\) where \(p(x),q(x)\) are coprime polynomials of \(K=F(x)\) is fixed under \(\sigma_M \circ \sigma_N\). Therefore following equality holds \[
\frac{p(x)}{q(x)}=z=(\sigma_2\circ\sigma_1)(z)=\frac{p(x+1)}{q(x+1)},\] which is equivalent to \[
p(x)q(x+1)=p(x+1)q(x).\] By induction, we get for \(n \in \mathbb Z\) \[
p(x)q(x+n)=p(x+n)q(x).\] Assume \(p(x)\) is not a constant polynomial. Then it has a root \(\alpha\) in some finite extension \(E\) of \(F\). As \(p(x),q(x)\) are coprime polynomials, \(q(\alpha) \neq 0\). Consequently \(p(\alpha+n)=0\) for all \(n \in \mathbb Z\) and the elements \(\alpha +n\) are all distinct as the characteristic of \(F\) is supposed to be non zero. This implies that \(p(x)\) is the zero polynomial, in contradiction with our assumption. Therefore \(p(x)\) is a constant polynomial and \(q(x)\) also according to a similar proof. Hence \(z\) is constant as was supposed to be proven.

Finally, \(K=F(x)\) is not algebraic over \(F=M \cap N\) as \((1,x, x^2, \dots, x^n, \dots)\) is independent over the field \(F\) which concludes our claims on \(K, M\) and \(N\).

Algebra

Complex matrix without a square root

Leave a comment

Consider for \(n \ge 2\) the linear space \(\mathcal M_n(\mathbb C)\) of complex matrices of dimension \(n \times n\). Is a matrix \(T \in \mathcal M_n(\mathbb C)\) always having a square root \(S \in \mathcal M_n(\mathbb C)\), i.e. a matrix such that \(S^2=T\)? is the question we deal with.

First, one can note that if \(T\) is similar to \(V\) with \(T = P^{-1} V P\) and \(V\) has a square root \(U\) then \(T\) also has a square root as \(V=U^2\) implies \(T=\left(P^{-1} U P\right)^2\).

Diagonalizable matrices

Suppose that \(T\) is similar to a diagonal matrix \[
D=\begin{bmatrix}
d_1 & 0 & \dots & 0 \\
0 & d_2 & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n
\end{bmatrix}\] Any complex number has two square roots, except \(0\) which has only one. Therefore, each \(d_i\) has at least one square root \(d_i^\prime\) and the matrix \[
D^\prime=\begin{bmatrix}
d_1^\prime & 0 & \dots & 0 \\
0 & d_2^\prime & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n^\prime
\end{bmatrix}\] is a square root of \(D\). Continue reading Complex matrix without a square root →

Algebra

Additive subgroups of vector spaces

Leave a comment

Consider a vector space \(V\) over a field \(F\). A subspace \(W \subseteq V\) is an additive subgroup of \((V,+)\). The converse might not be true.

If the characteristic of the field is zero, then a subgroup \(W\) of \(V\) might not be an additive subgroup. For example \(\mathbb R\) is a vector space over \(\mathbb R\) itself. \(\mathbb Q\) is an additive subgroup of \(\mathbb R\). However \(\sqrt{2}= \sqrt{2}.1 \notin \mathbb Q\) proving that \(\mathbb Q\) is not a subspace of \(\mathbb R\).

Another example is \(\mathbb Q\) which is a vector space over itself. \(\mathbb Z\) is an additive subgroup of \(\mathbb Q\), which is not a subspace as \(\frac{1}{2} \notin \mathbb Z\).

Yet, an additive subgroup of a vector space over a prime field \(\mathbb F_p\) with \(p\) prime is a subspace. To prove it, consider an additive subgroup \(W\) of \((V,+)\) and \(x \in W\). For \(\lambda \in F\), we can write \(\lambda = \underbrace{1 + \dots + 1}_{\lambda \text{ times}}\). Consequently \[
\lambda \cdot x = (1 + \dots + 1) \cdot x= \underbrace{x + \dots + x}_{\lambda \text{ times}} \in W.\]

Finally an additive subgroup of a vector space over any finite field is not always a subspace. For a counterexample, take the non-prime finite field \(\mathbb F_{p^2}\) (also named \(\text{GF}(p^2)\)). \(\mathbb F_{p^2}\) is also a vector space over itself. The prime finite field \(\mathbb F_p \subset \mathbb F_{p^2}\) is an additive subgroup that is not a subspace of \(\mathbb F_{p^2}\).

Algebra

Non commutative rings

Leave a comment

Let’s recall that a set \(R\) equipped with two operations \((R,+,\cdot)\) is a ring if and only if \((R,+)\) is an abelian group, multiplication \(\cdot\) is associative and has a multiplicative identity \(1\) and multiplication is left and right distributive with respect to addition.

\((\mathbb Z, +, \cdot)\) is a well known infinite ring which is commutative. The rational, real and complex numbers are other infinite commutative rings. Those are in fact fields as every non-zero element have a multiplicative inverse.

For a field \(F\) (finite or infinite), the polynomial ring \(F[X]\) is another example of infinite commutative ring.

Also for \(n\) integer, the integers modulo n is a finite ring that is commutative. Finally, according to Wedderburn theorem every finite division ring is commutative.

So what are examples of non commutative rings? Let’s provide a couple. Continue reading Non commutative rings →

Algebra

A linear map without any minimal polynomial

Leave a comment

Given an endomorphism \(T\) on a finite-dimensional vector space \(V\) over a field \(\mathbb F\), the minimal polynomial \(\mu_T\) of \(T\) is well defined as the generator (unique up to units in \(\mathbb F\)) of the ideal:\[
I_T= \{p \in \mathbb F[t]\ ; \ p(T)=0\}.\]

For infinite-dimensional vector spaces, the minimal polynomial might not be defined. Let’s provide an example.

We take the real polynomials \(V = \mathbb R [t]\) as a real vector space and consider the derivative map \(D : P \mapsto P^\prime\). Let’s prove that \(D\) doesn’t have any minimal polynomial. By contradiction, suppose that \[
\mu_D(t) = a_0 + a_1 t + \dots + a_n t^n \text{ with } a_n \neq 0\] is the minimal polynomial of \(D\), which means that for all \(P \in \mathbb R[t]\) we have \[
a_0 + a_1 P^\prime + \dots + a_n P^{(n)} = 0.\] Taking for \(P\) the polynomial \(t^n\) we get \[
a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n = 0,\] which doesn’t make sense as \(n! a_n \neq 0\), hence \(a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n\) cannot be the zero polynomial.

We conclude that \(D\) doesn’t have any minimal polynomial.

Algebra

Non linear map preserving Euclidean norm

Leave a comment

Let \(V\) be a real vector space endowed with an Euclidean norm \(\Vert \cdot \Vert\).

A bijective map \( T : V \to V\) that preserves inner product \(\langle \cdot, \cdot \rangle\) is linear. Also, Mazur-Ulam theorem states that an onto map \( T : V \to V\) which is an isometry (\( \Vert T(x)-T(y) \Vert = \Vert x-y \Vert \) for all \(x,y \in V\)) and fixes the origin (\(T(0) = 0\)) is linear.

What about an application that preserves the norm (\(\Vert T(x) \Vert = \Vert x \Vert\) for all \(x \in V\))? \(T\) might not be linear as we show with following example:\[
\begin{array}{l|rcll}
T : & V & \longrightarrow & V \\
& x & \longmapsto & x & \text{if } \Vert x \Vert \neq 1\\
& x & \longmapsto & -x & \text{if } \Vert x \Vert = 1\end{array}\]

It is clear that \(T\) preserves the norm. However \(T\) is not linear as soon as \(V\) is not the zero vector space. In that case, consider \(x_0\) such that \(\Vert x_0 \Vert = 1\). We have:\[
\begin{cases}
T(2 x_0) &= 2 x_0 \text{ as } \Vert 2 x_0 \Vert = 2\\
\text{while}\\
T(x_0) + T(x_0) = -x_0 + (-x_0) &= – 2 x_0
\end{cases}\]

Algebra

Non linear map preserving orthogonality

Leave a comment

Let \(V\) be a real vector space endowed with an inner product \(\langle \cdot, \cdot \rangle\).

It is known that a bijective map \( T : V \to V\) that preserves the inner product \(\langle \cdot, \cdot \rangle\) is linear.

That might not be the case if \(T\) is supposed to only preserve orthogonality. Let’s consider for \(V\) the real plane \(\mathbb R^2\) and the map \[
\begin{array}{l|rcll}
T : & \mathbb R^2 & \longrightarrow & \mathbb R^2 \\
& (x,y) & \longmapsto & (x,y) & \text{for } xy \neq 0\\
& (x,0) & \longmapsto & (0,x)\\
& (0,y) & \longmapsto & (y,0) \end{array}\]

The restriction of \(T\) to the plane less the x-axis and the y-axis is the identity and therefore is bijective on this set. Moreover \(T\) is a bijection from the x-axis onto the y-axis, and a bijection from the y-axis onto the x-axis. This proves that \(T\) is bijective on the real plane.

\(T\) preserves the orthogonality on the plane less x-axis and y-axis as it is the identity there. As \(T\) swaps the x-axis and the y-axis, it also preserves orthogonality of the coordinate axes. However, \(T\) is not linear as for non zero \(x \neq y\) we have: \[
\begin{cases}
T[(x,0) + (0,y)] = T[(x,y)] &= (x,y)\\
\text{while}\\
T[(x,0)] + T[(0,y)] = (0,x) + (y,0) &= (y,x)
\end{cases}\]

Algebra

A simple ring which is not a division ring

Leave a comment

Let’s recall that a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. A division ring is a simple ring. Is the converse true? The answer is negative and we provide here a counterexample of a simple ring which is not a division ring.

We prove that for \(n \ge 1\) the matrix ring \(M_n(F)\) of \(n \times n\) matrices over a field \(F\) is simple. \(M_n(F)\) is obviously not a division ring as the matrix with \(1\) at position \((1,1)\) and \(0\) elsewhere is not invertible.

Let’s prove first following lemma. Continue reading A simple ring which is not a division ring →

Algebra

Unique factorization domain that is not a Principal ideal domain

Leave a comment

In this article, we provide an example of a unique factorization domain – UFD that is not a principal ideal domain – PID. However, it is known that a PID is a UFD.

We take a field \(F\), for example \(\mathbb Q\), \(\mathbb R\), \(\mathbb F_p\) (where \(p\) is a prime) or whatever more exotic.

The polynomial ring \(F[X]\) is a UFD. This follows from the fact that \(F[X]\) is a Euclidean domain. It is also known that for a UFD \(R\), \(R[X]\) is also a UFD. Therefore the polynomial ring \(F[X_1,X_2]\) in two variables is a UFD as \(F[X_1,X_2] = F[X_1][X_2]\). However the ideal \(I=(X_1,X_2)\) is not principal. Let’s prove it by contradiction.

Suppose that \((X_1,X_2) = (P)\) with \(P \in F[X_1,X_2]\). Then there exist two polynomials \(Q_1,Q_2 \in F[X_1,X_2]\) such that \(X_1=PQ_1\) and \(X_2=PQ_2\). As a polynomial in variable \(X_2\), the polynomial \(X_1\) is having degree \(0\). Therefore, the degree of \(P\) as a polynomial in variable \(X_2\) is also equal to \(0\). By symmetry, we get that the degree of \(P\) as a polynomial in variable \(X_1\) is equal to \(0\) too. Which implies that \(P\) is an element of the field \(F\) and consequently that \((X_1,X_2) = F[X_1,X_2]\).

But the equality \((X_1,X_2) = F[X_1,X_2]\) is absurd. Indeed, the degree of a polynomial \(X_1 T_1 + X_2 T_2\) cannot be equal to \(0\) for any \(T_1,T_2 \in F[X_1,X_2]\). And therefore \(1 \notin F[X_1,X_2]\).