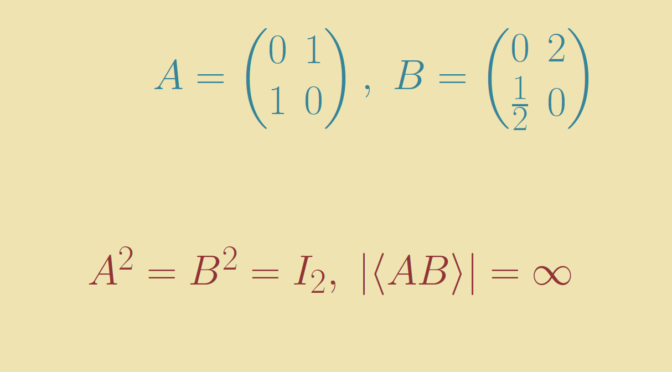Consider a group \(G\) and have a look at the question: is the subset \(S\) of elements of finite order a subgroup of \(G\)?
The answer is positive when any two elements of \(S\) commute. For the proof, consider \(x,y \in S\) of order \(m,n\) respectively. Then \[
\left(xy\right)^{mn} = x^{mn} y^{mn} = (x^m)^n (y^n)^m = e\] where \(e\) is the identity element. Hence \(xy\) is of finite order (less or equal to \(mn\)) and belong to \(S\).
Example of a non abelian group
In that cas, \(S\) might not be subgroup of \(G\). Let’s take for \(G\) the general linear group over \(\mathbb Q\) (the set of rational numbers) of \(2 \times 2\) invertible matrices named \(\text{GL}_2(\mathbb Q)\). The matrices \[
A = \begin{pmatrix}0&1\\1&0\end{pmatrix},\ B=\begin{pmatrix}0 & 2\\\frac{1}{2}& 0\end{pmatrix}\] are of order \(2\). They don’t commute as \[
AB = \begin{pmatrix}\frac{1}{2}&0\\0&2\end{pmatrix} \neq \begin{pmatrix}2&0\\0&\frac{1}{2}\end{pmatrix}=BA.\] Finally, \(AB\) is of infinite order and therefore doesn’t belong to \(S\) proving that \(S\) is not a subgroup of \(G\).