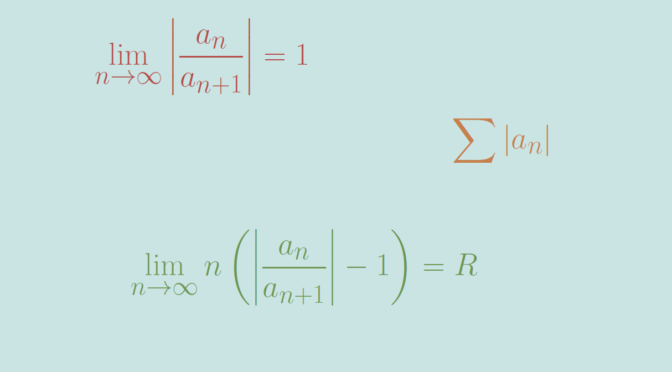The Raabe-Duhamel’s test (also named Raabe’s test) is a test for the convergence of a series \[
\sum_{n=1}^\infty a_n \] where each term is a real or complex number. The Raabe-Duhamel’s test was developed by Swiss mathematician Joseph Ludwig Raabe.

It states that if:

\[\displaystyle \lim _{n\to \infty }\left\vert{\frac {a_{n}}{a_{n+1}}}\right\vert=1 \text{ and } \lim _{{n\to \infty }} n \left(\left\vert{\frac {a_{n}}{a_{{n+1}}}}\right\vert-1 \right)=R,\]
then the series will be absolutely convergent if \(R > 1\) and divergent if \(R < 1\). First one can notice that Raabe-Duhamel's test maybe conclusive in cases where ratio test isn't. For instance, consider a real \(\alpha\) and the series \(u_n=\frac{1}{n^\alpha}\). We have \[ \lim _{n\to \infty } \frac{u_{n+1}}{u_n} = \lim _{n\to \infty } \left(\frac{n}{n+1} \right)^\alpha = 1\] and therefore the ratio test is inconclusive. However \[ \frac{u_n}{u_{n+1}} = \left(\frac{n+1}{n} \right)^\alpha = 1 + \frac{\alpha}{n} + o \left(\frac{1}{n}\right)\] for \(n\) around \(\infty\) and \[ \lim _{{n\to \infty }} n \left(\frac {u_{n}}{u_{{n+1}}}-1 \right)=\alpha.\] Raabe-Duhamel's test allows to conclude that the series \(\sum u_n\) diverges for \(\alpha <1\) and converges for \(\alpha > 1\) as well known.

When \(R=1\) in the Raabe’s test, the series can be convergent or divergent. For example, the series above \(u_n=\frac{1}{n^\alpha}\) with \(\alpha=1\) is the harmonic series which is divergent.

On the other hand, the series \(v_n=\frac{1}{n \log^2 n}\) is convergent as can be proved using the integral test. Namely \[
0 \le \frac{1}{n \log^2 n} \le \int_{n-1}^n \frac{dt}{t \log^2 t} \text{ for } n \ge 3\] and \[
\int_2^\infty \frac{dt}{t \log^2 t} = \left[-\frac{1}{\log t} \right]_2^\infty = \frac{1}{\log 2}\] is convergent, while \[
\frac{v_n}{v_{n+1}} = 1 + \frac{1}{n} +\frac{2}{n \log n} + o \left(\frac{1}{n \log n}\right)\] for \(n\) around \(\infty\) and therefore \(R=1\) in the Raabe-Duhamel’s test.