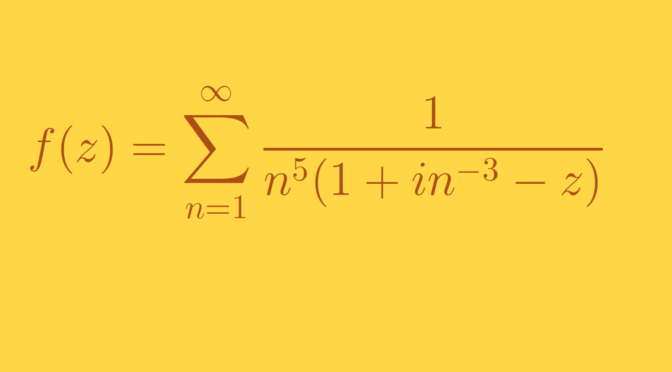Consider a complex power series \(\displaystyle \sum_{k=0}^\infty a_k z^k\) with radius of convergence \(0 \lt R \lt \infty\) and suppose that for every \(w\) with \(\vert w \vert = R\), \(\displaystyle \sum_{k=0}^\infty a_k w^k\) converges.

We provide an example where the power expansion at the origin \[
\displaystyle f(z) = \sum_{k=0}^\infty a_k z^k\] is discontinuous on the closed disk \(\vert z \vert \le R \).

The function \(f\) is constructed as an infinite sum \[
\displaystyle f(z) = \sum_{n=1}^\infty f_n(z)\] with \(f_n(z) = \frac{\delta_n}{a_n-z}\) where \((\delta_n)_{n \in \mathbb N}\) is a sequence of positive real numbers and \((a_n)\) a sequence of complex numbers of modulus larger than one and converging to one. Let \(f_n^{(r)}(z)\) denote the sum of the first \(r\) terms in the power series expansion of \(f_n(z)\) and \(\displaystyle f^{(r)}(z) \equiv \sum_{n=1}^\infty f_n^{(r)}(z)\).

We’ll prove that:

1. If \(\sum_n \delta_n \lt \infty\) then \(\sum_{n=1}^\infty f_n^{(r)}(z)\) converges and \(f(z) = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(z)\) for \(\vert z \vert \le 1\) and \(z \neq 1\).
2. If \(a_n=1+i \epsilon_n\) and \(\sum_n \delta_n/\epsilon_n < \infty\) then \(\sum_{n=1}^\infty f_n^{(r)}(1)\) converges and \(f(1) = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(1)\)
3. If \(\delta_n/\epsilon_n^2 \to \infty\) then \(f(z)\) is unbounded on the disk \(\vert z \vert \le 1\).

First, let’s recall this corollary of Lebesgue’s dominated convergence theorem:

Let \((u_{n,i})_{(n,i) \in \mathbb N \times \mathbb N}\) be a double sequence of complex numbers. Suppose that \(u_{n,i} \to v_i\) for all \(i\) as \(n \to \infty\), and that \(\vert u_{n,i} \vert \le w_i\) for all \(n\) with \(\sum_i w_i < \infty\). Then for all \(n\) the series \(\sum_i u_{n,i}\) is absolutely convergent and \(\lim_n \sum_i u_{n,i} = \sum_i v_i\).

Proof of result (1)

Let’s fix \(\vert z \vert \le 1\) with \(z \neq 1\). The sum of the first \(r\) terms in the power series expansion of \(f_n(z)\) about the origin is equal to \[
f_n^{(r)}(z) = \delta_n \frac{1-\left( z/a_n \right)^r}{a_n-z}.\] As \(\vert a_n \vert > 1\) we have \[
\left\vert f_n^{(r)}(z) \right\vert = \left\vert \delta_n \frac{1-\left( z/a_n \right)^r}{a_n-z} \right\vert \le \frac{2 \delta_n}{\vert a_n – z \vert}\]

And as \(\lim_n a_n = 1\), the right hand side of above inequality is bounded by a multiple of \(\delta_n\). With the hypothesis \(\sum_n \delta_n < \infty\) that proves that the series \(\sum_n f_n^{(r)}(z)\) is absolutely convergent for all \(r \ge 0\). Also for all \(n \in \mathbb N\) we have \[ \lim\limits_{r \to \infty} f_n^{(r)}(z) = \lim\limits_{r \to \infty} \delta_n \frac{1-\left( z/a_n \right)^r}{a_n-z} = \frac{\delta_n}{a_n-z}.\] Using the corollary of the dominated converge theorem mentioned above we get \[ f(z) = \sum_{n=1}^\infty \frac{\delta_n}{a_n-z} = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(z)\] proving that \(f(z)\) is a power series on the open disk \(\vert z \vert <1\) converging on its circle of convergence for all \(z \neq 1\).

Proof of result (2)

Let’s now consider the case \(z = 1\). We have \[
\left\vert f_n^{(r)}(1) \right\vert = \left\vert \delta_n \frac{1-\left( 1/a_n \right)^r}{a_n-1} \right\vert \le \frac{2 \delta_n}{\epsilon_n}\] as \(\vert a_n – 1 \vert = \epsilon_n\) for all \(n \in \mathbb N\). With the hypothesis \(\sum_n \delta_n/\epsilon_n < \infty\), we get that \(\sum_n f_n^{(r)}(1)\) is absolutely convergent for all \(r \ge 0\). Applying again dominated convergence theorem, we find that that the power series of \(f(z)\) about the origin converges for \(z=1\).

Proof of result (3)

Finally we have to prove that \(f(z)\) is unbounded on the disk \(\vert z \vert \le 1\) if \(\delta_n/\epsilon_n^2 \to \infty\).

For \(m \in \mathbb N\) the real part of \(\frac{1}{a_m – z}\) is \(\frac{1- \Re z}{\vert a_m – z \vert^2}\), hence is non negative for \(\vert z \vert \le 1\). While for \(q_n=a_n/ \left\vert a_n \right\vert\): \[
\Re f(q_n) \ge \Re f_n(q_n)=\frac{\delta_n}{\sqrt{1+\epsilon_n^2}(\sqrt{1+\epsilon_n^2}-1)}\ge\frac{2\delta_n}{\epsilon_n^2\sqrt{1+\epsilon_n^2}}.\] If \(\delta_n/\epsilon_n^2 \to \infty\) we conclude that \(\Re f(q_n)\) diverges to \(\infty\).

A precise example

An example of function satisfying the three conditions mentioned above is \[
f(z)=\sum_{n=1}^\infty\frac1{n^5(1+in^{-3}-z)}
\] for which

• \(\delta_n = \frac{1}{n^5}\)
• \(a_n = 1 + i n^{-3}\)

The origin of this article is this MathOverflow article.