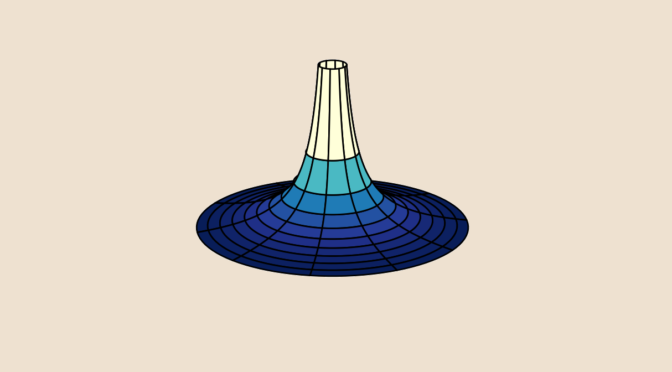
Can you paint a surface with infinite area with a finite quantity of paint? For sure… let’s do it!

Consider the 3D surface given in cylindrical coordinates as $$S(\rho,\varphi):\begin{cases} x &= \rho \cos \varphi\\ y &= \rho \sin \varphi\\ z &= \frac{1}{\rho}\end{cases}$$ for $(\rho,\varphi) \in [1,\infty) \times [0, 2 \pi)$. The surface is named Gabriel’s horn.

Volume of Gabriel’s horn

The volume of Gabriel’s horn is $$V = \pi \int_1^\infty \left( \frac{1}{\rho^2} \right) \ d\rho = \pi$$ which is finite.

Area of Gabriel’s horn

The area of Gabriel’s horn for $(\rho,\varphi) \in [1,a) \times [0, 2 \pi)$ with $a > 1$ is: $$A = 2 \pi \int_1^a \frac{1}{\rho} \sqrt{1+\left( -\frac{1}{\rho^2} \right)^2} \ d\rho \ge 2 \pi \int_1^a \frac{d \rho}{\rho} = 2 \pi \log a.$$ As the right hand side of inequality above diverges to $\infty$ as $a \to \infty$, we can conclude that the area of Gabriel’s horn is infinite.

Conclusion

Gabriel’s horn could be filled with a finite quantity of paint… therefore painting a surface with infinite area. Unfortunately the thickness of the paint coat is converging to $0$ as $z$ goes to $\infty$, leading to a paint which won’t be too visible!