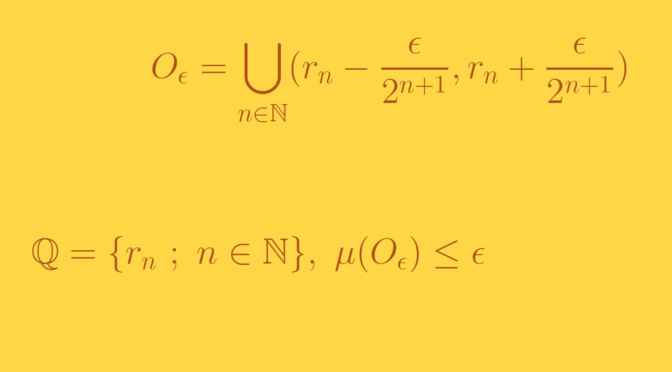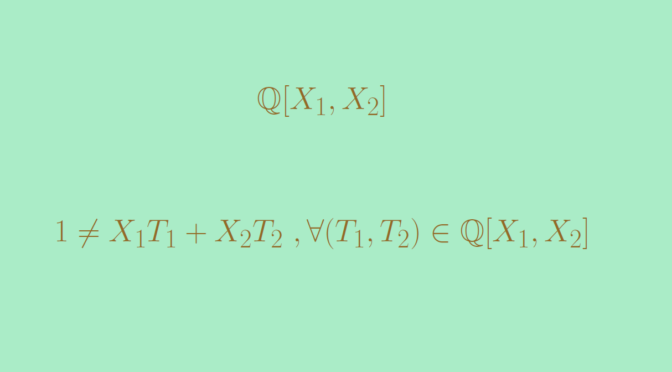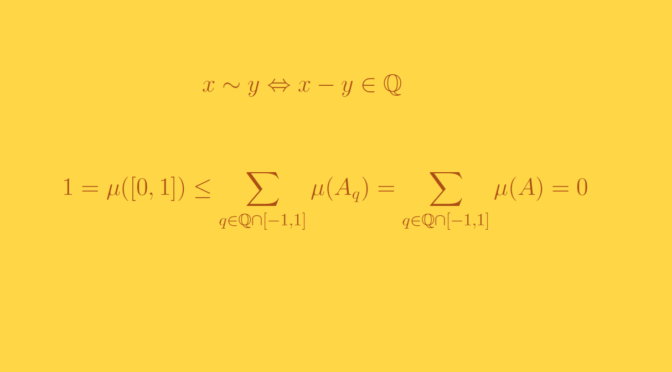Set Theory

Small open sets containing the rationals

Leave a comment

The set \(\mathbb Q\) of the rational number is countable infinite and dense in \(\mathbb R\). You can have a look here on a way to build a bijective map between \(\mathbb N\) and \(\mathbb Q\).

Now given \(\epsilon > 0\), can one find an open set \(O_\epsilon\) of measure less than \(\epsilon\) with \(\mathbb Q \subseteq O_\epsilon\)?

The answer is positive. Let’s denote \[
O_\epsilon = \bigcup_{n \in \mathbb N} (r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\] where \((r_n)_{n \in \mathbb N}\) is an enumeration of the rationals. Obviously \(\mathbb Q \subseteq O_\epsilon\). Using countable subadditivity of Lebesgue measure \(\mu\), we get:
\begin{align*}
\mu(O_\epsilon) &\le \sum_{n \in \mathbb N} \mu((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}}))\\
&= \sum_{n \in \mathbb N} \frac{2 \epsilon}{2^{n+1}} = \sum_{n \in \mathbb N} \frac{\epsilon}{2^n} = \epsilon
\end{align*}

Therefore we’re done. Some additional comments:

  • While Lebesgue measure of the reals is infinite and the rationals are dense in the reals, we can include the rationals in an open set of measure as small as desired!
  • The open segments \((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\) are overlapping. Hence \(\mu(O_\epsilon)\) is strictly less than \(\epsilon\).
Analysis

A continuous function with divergent Fourier series

1 Comment

It is known that for a piecewise continuously differentiable function \(f\), the Fourier series of \(f\) converges at all \(x \in \mathbb R\) to \(\frac{f(x^-)+f(x^+)}{2}\).

We describe Fejér example of a continuous function with divergent Fourier series. Fejér example is the even, \((2 \pi)\)-periodic function \(f\) defined on \([0,\pi]\) by: \[
f(x) = \sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\]
According to Weierstrass M-test, \(f\) is continuous. We denote \(f\) Fourier series by \[
\frac{1}{2} a_0 + (a_1 \cos x + b_1 \sin x) + \dots + (a_n \cos nx + b_n \sin nx) + \dots.\]

As \(f\) is even, the \(b_n\) are all vanishing. If we denote for all \(m \in \mathbb N\):\[
\lambda_{n,m}=\int_0^{\pi} \sin \left[ (2m + 1) \frac{t}{2} \right] \cos nt \ dt \text{ and } \sigma_{n,m} = \sum_{k=0}^n \lambda_{k,m},\]
we have:\[
\begin{aligned}
a_n &=\frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \cos nt \ dt= \frac{2}{\pi} \int_0^{\pi} f(t) \cos nt \ dt\\
&= \frac{2}{\pi} \int_0^{\pi} \left(\sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\right) \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \int_0^{\pi} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right] \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \lambda_{n,2^{p^3-1}}
\end{aligned}\] One can switch the \(\int\) and \(\sum\) signs as the series is normally convergent.

We now introduce for all \(n \in \mathbb N\):\[
S_n = \frac{\pi}{2} \sum_{k=0}^n a_k = \sum_{p=1}^\infty \sum_{k=0}^n \frac{1}{p^2} \lambda_{k,2^{p^3-1}}
=\sum_{p=1}^\infty \frac{1}{p^2} \sigma_{n,2^{p^3-1}}\]

We will prove below that for all \(n,m \in \mathbb N\) we have \(\sigma_{m,m} \ge \frac{1}{2} \ln m\) and \(\sigma_{n,m} \ge 0\). Assuming those inequalities for now, we get:\[
S_{2^{p^3-1}} \ge \frac{1}{p^2} \sigma_{2^{p^3-1},2^{p^3-1}} \ge \frac{1}{2p^2} \ln(2^{p^3-1}) = \frac{p^3-1}{2p^2} \ln 2\]
As the right hand side diverges to \(\infty\), we can conclude that \((S_n)\) diverges and consequently that the Fourier series of \(f\) diverges at \(0\). Continue reading A continuous function with divergent Fourier series →

Analysis

Radius of convergence of power series

Leave a comment

We look here at the radius of convergence of the sum and product of power series.

Let’s recall that for a power series \(\displaystyle \sum_{n=0}^\infty a_n x^n\) where \(0\) is not the only convergence point, the radius of convergence is the unique real \(0 < R \le \infty\) such that the series converges whenever \(\vert x \vert < R\) and diverges whenever \(\vert x \vert > R\).

Given two power series with radii of convergence \(R_1\) and \(R_2\), i.e.
\begin{align*}
\displaystyle f_1(x) = \sum_{n=0}^\infty a_n x^n, \ \vert x \vert < R_1 \\ \displaystyle f_2(x) = \sum_{n=0}^\infty b_n x^n, \ \vert x \vert < R_2 \end{align*} The sum of the power series \begin{align*} \displaystyle f_1(x) + f_2(x) &= \sum_{n=0}^\infty a_n x^n + \sum_{n=0}^\infty b_n x^n \\ &=\sum_{n=0}^\infty (a_n + b_n) x^n \end{align*} and its Cauchy product:
\begin{align*}
\displaystyle f_1(x) \cdot f_2(x) &= \left(\sum_{n=0}^\infty a_n x^n\right) \cdot \left(\sum_{n=0}^\infty b_n x^n \right) \\
&=\sum_{n=0}^\infty \left( \sum_{l=0}^n a_l b_{n-l}\right) x^n
\end{align*}
both have radii of convergence greater than or equal to \(\min \{R_1,R_2\}\).

The radii can indeed be greater than \(\min \{R_1,R_2\}\). Let’s give examples.
Continue reading Radius of convergence of power series →

Set Theory

A partially ordered set having multiple minimal elements

Leave a comment

Let’s consider a partially ordered set (or poset) \(E\).

If \(E\) is totally ordered, \(E\) has at most one minimal element. If \(E\) is not totally ordered, \(E\) can have multiple minimal elements. We provide an example for the set \(E=\{n \in \mathbb N \ | \ n \ge 2\}\). For two natural numbers \(n\) and \(m\), we write \(n|m\) if \(n\) divides \(m\). One easily sees that this yields a partial order.

The minimal elements of \(E\) are the elements not having divisors, this is the case for all prime numbers \(p \in E\).

\(E\) has an infinite number of minimal elements which are the prime numbers.

Algebra

Unique factorization domain that is not a Principal ideal domain

Leave a comment

In this article, we provide an example of a unique factorization domain – UFD that is not a principal ideal domain – PID. However, it is known that a PID is a UFD.

We take a field \(F\), for example \(\mathbb Q\), \(\mathbb R\), \(\mathbb F_p\) (where \(p\) is a prime) or whatever more exotic.

The polynomial ring \(F[X]\) is a UFD. This follows from the fact that \(F[X]\) is a Euclidean domain. It is also known that for a UFD \(R\), \(R[X]\) is also a UFD. Therefore the polynomial ring \(F[X_1,X_2]\) in two variables is a UFD as \(F[X_1,X_2] = F[X_1][X_2]\). However the ideal \(I=(X_1,X_2)\) is not principal. Let’s prove it by contradiction.

Suppose that \((X_1,X_2) = (P)\) with \(P \in F[X_1,X_2]\). Then there exist two polynomials \(Q_1,Q_2 \in F[X_1,X_2]\) such that \(X_1=PQ_1\) and \(X_2=PQ_2\). As a polynomial in variable \(X_2\), the polynomial \(X_1\) is having degree \(0\). Therefore, the degree of \(P\) as a polynomial in variable \(X_2\) is also equal to \(0\). By symmetry, we get that the degree of \(P\) as a polynomial in variable \(X_1\) is equal to \(0\) too. Which implies that \(P\) is an element of the field \(F\) and consequently that \((X_1,X_2) = F[X_1,X_2]\).

But the equality \((X_1,X_2) = F[X_1,X_2]\) is absurd. Indeed, the degree of a polynomial \(X_1 T_1 + X_2 T_2\) cannot be equal to \(0\) for any \(T_1,T_2 \in F[X_1,X_2]\). And therefore \(1 \notin F[X_1,X_2]\).

Set Theory

A non-measurable set

Leave a comment

We describe here a non-measurable subset of the segment \(I=[0,1] \subset \mathbb R\).

Let’s define on \(I\) an equivalence relation by \(x \sim y\) if and only if \(x-y \in \mathbb Q\). The equivalence relation \(\sim\) induces equivalence classes on \(I\). For \(x \in I\), it’s equivalence class \([x]\) is \([x] = \{y \in I \ : \ y-x \in \mathbb Q\}\). By the Axiom of Choice, we can form a set \(A\) by selecting a single point from each equivalence class.

We claim that the set \(A\) is not Lebesgue measurable.

For all \(q \in \mathbb Q\) we denote \(A_q = \{q+x \ : x \in A\}\). Let’s take \(p,q \in \mathbb Q\). If it exists \(z \in A_p \cap A_q\), it means that there exist \(u,v \in A\) such that
\[z= p+u=q+v\] hence \(u-v=q-p=0\) as \(u,v\) are supposed to be unique representatives of the classes of the equivalence relation \(\sim\). Finally if \(p,q\) are distincts, \(A_p \cap A_q = \emptyset\).

As Lebesgue measure \(\mu\) is translation invariant, we have for \(q \in \mathbb Q \cap [0,1]\) : \(\mu(A) = \mu(A_q)\) and also \(A_q \subset [0,2]\). Hence if we denote
\[B = \bigcup_{q \in \mathbb Q \cap [0,1]} A_q\] we have \(B \subset [0,2]\). If we suppose that \(A\) is measurable, we get
\[\mu(B) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A) \le 2\] by countable additivity of Lebesgue measure (the set \(\mathbb Q \cap [0,1]\) being countable infinite). This implies \(\mu(A) = 0\).

Let’s prove now that
\[[0,1] \subset \bigcup_{q \in \mathbb Q \cap [-1,1]} A_q\] For \(z \in [0,1]\), there exists \(u \in A\) such that \(z \in [u]\). As \(A \subset [0,1]\), we have \(q = z-u \in \mathbb Q\) and \(-1 \le q \le 1\). And \(z=q+u\) means that \(z \in A_q\). This proves the inclusion. However the inclusion implies the contradiction
\[1 = \mu([0,1]) \le \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A) =0\]

Finally \(A\) is not Lebesgue measurable.

Topology

Isometric versus affine

Leave a comment

Throughout this article we let \(E\) and \(F\) denote real normed vector spaces. A map \(f : E \rightarrow F\) is an isometry if \(\Vert f(x) – f(y) \Vert = \Vert x – y \Vert\) for all \(x, y \in E\), and \(f\) is affine if \[
f((1-t) a + t b ) = (1-t) f(a) + t f(b) \] for all \(a,b \in E\) and \(t \in [0,1]\). Equivalently, \(f\) is affine if the map \(T : E \rightarrow F\), defined by \(T(x)=f(x)-f(0)\) is linear.

First note that an isometry \(f\) is always one-to-one as \(f(x) = f(y)\) implies \[
0 = \Vert f(x) – f(y) \Vert = \Vert x- y \Vert\] hence \(x=y\).

There are two important cases when every isometry is affine:

  1. \(f\) is bijective (equivalently surjective). This is Mazur-Ulam theorem, which was proven in 1932.
  2. \(F\) is a strictly convex space. Recall that a normed vector space \((S, \Vert \cdot \Vert)\) is strictly convex if and only if for all distinct \(x,y \in S\), \(\Vert x \Vert = \Vert y \Vert =1\) implies \(\Vert \frac{x+y}{2} \Vert <1\). For example, an inner product space is strictly convex. The sequence spaces \(\ell_p\) for \(1 < p < \infty\) are also strictly convex.

Continue reading Isometric versus affine →

Analysis

Counterexample around Morera’s theorem

Leave a comment

Let’s recall Morera’s theorem.

Morera’s theorem Suppose that \(f\) is a continuous complex-valued function in a connected open set \(\Omega \subset \mathbb C\) such that
\[\int_{\partial \Delta} f(z) \ dz = 0\] for every closed triangle \(\Delta \subset \Omega \setminus \{p\}\) where \(p \in \Omega\). Then \(f\) is holomorphic in \(\Omega\).

Does the conclusion of Morera’s theorem still hold if \(f\) is supposed to be continuous only in \(\Omega \setminus \{p\}\)? The answer is negative and we provide a counterexample.

Let \(\Omega\) be the entire complex plane, \(f\) defined as follows
\[f(z)=\begin{cases}
\frac{1}{z^2} & \text{if } z \neq 0\\
0 & \text{otherwise}
\end{cases}\] and \(p\) the origin.

For \(a,b \in \Omega \setminus \{0\}\) we have
\[\begin{aligned}
\int_{[a,b]} f(z) \ dz &= \int_{[a,b]} \frac{dz}{z^2}\\
&= \int_0^1 \frac{b-a}{[a+t(b-a)]^2} \ dt\\
&=\left[ -\frac{1}{a+t(b-a)} \right]_0^1 = \frac{1}{a} – \frac{1}{b}
\end{aligned}\]

Hence for a triangle \(\Delta\) with vertices at \(a,b ,c \in \Omega \setminus \{0\}\):
\[\int_{\partial \Delta} f(z) \ dz = \left( \frac{1}{a} – \frac{1}{b} \right) + \left( \frac{1}{b} – \frac{1}{c} \right) + \left( \frac{1}{c} – \frac{1}{a} \right)=0\]

However, \(f\) is not holomorphic in \(\Omega\) as it is even not continuous at \(0\).

Analysis

Continuity versus uniform continuity

Leave a comment

We consider real-valued functions.

A real-valued function \(f : I \to \mathbb R\) (where \(I \subseteq\) is an interval) is continuous at \(x_0 \in I\) when: \[(\forall \epsilon > 0) (\exists \delta > 0)(\forall x \in I)(\vert x- x_0 \vert \le \delta \Rightarrow \vert f(x)- f(x_0) \vert \le \epsilon).\] When \(f\) is continuous at all \(x \in I\), we say that \(f\) is continuous on \(I\).

\(f : I \to \mathbb R\) is said to be uniform continuity on \(I\) if \[(\forall \epsilon > 0) (\exists \delta > 0)(\forall x,y \in I)(\vert x- y \vert \le \delta \Rightarrow \vert f(x)- f(y) \vert \le \epsilon).\]

Obviously, a function which is uniform continuous on \(I\) is continuous on \(I\). Is the converse true? The answer is negative.

An (unbounded) continuous function which is not uniform continuous

The map \[
\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x^2 \end{array}\] is continuous. Let’s prove that it is not uniform continuous. For \(0 < x < y\) we have \[\vert f(x)-f(y) \vert = y^2-x^2 = (y-x)(y+x) \ge 2x (y-x)\] Hence for \(y-x= \delta >0\) and \(x = \frac{1}{\delta}\) we get
\[\vert f(x) -f(y) \vert \ge 2x (y-x) =2 > 1\] which means that the definition of uniform continuity is not fulfilled for \(\epsilon = 1\).

For this example, the function is unbounded as \(\lim\limits_{x \to \infty} x^2 = \infty\). Continue reading Continuity versus uniform continuity →

Mathematical exceptions to the rules or intuition