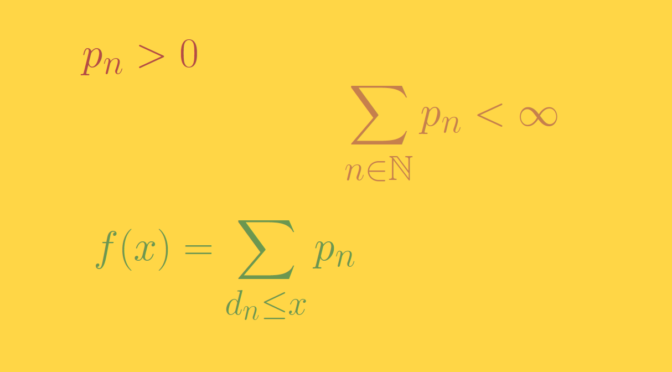Consider a compact interval \([a,b] \subset \mathbb R\) with \(a \lt b\). Let’s build an increasing function \(f : [a,b] \to \mathbb R\) whose points of discontinuity is an arbitrary dense subset \(D = \{d_n \ ; \ n \in \mathbb N\}\) of \([a,b]\), for example \(D = \mathbb Q \cap [a,b]\).

Let \(\sum p_n\) be a convergent series of positive numbers whose sum is equal to \(p\) and define \(\displaystyle f(x) = \sum_{d_n \le x} p_n\).

\(f\) is strictly increasing

For \(a \le x \lt y \le b\) we have \[
f(y) – f(x) = \sum_{x \lt d_n \le y} p_n \gt 0\] as the \(p_n\) are positive and dense so it exists \(p_m \in (x, y]\).

\(f\) is right-continuous on \([a,b]\)

We pick-up \(x \in [a,b]\). For any \(\epsilon \gt 0\) is exists \(N \in \mathbb N\) such that \(0 \lt \sum_{n \gt N} p_n \lt \epsilon\). Let \(\delta > 0\) be so small that the interval \((x,x+\delta)\) doesn’t contain any point in the finite set \(\{p_1, \dots, p_N\}\). Then \[
0 \lt f(y) – f(x) \le \sum_{n \gt N} p_n \lt \epsilon,\] for any \(y \in (x,x+\delta)\) proving the right-continuity of \(f\) at \(x\).

\(f\) is discontinuous at any \(x \in D\)

Suppose that \(x=d_m \in D\). We have for \(a \le y \lt x\) \[
f(x) -f(y) = \sum_{y \lt d_n \le x} p_n \gt p_m,\] proving that \(f\) is not left-continuous at \(x\).

\(f\) is continuous at all \(x \in [a,b] \setminus D\)

We only have to prove that \(f\) is left-continuous at \(x\). Let \(\mathbb N (x) = \{n \in \mathbb N \ ; \ d_n \lt x\}\). Then \(f(x) = \sum_{n \in \mathbb N(x)} p_n\) as \(x \notin D\). For an arbitrary \(\epsilon \gt 0\), it exists a finite subset \(\mathbb N_0 \subset \mathbb N(x)\) such that \(\sum_{n \in \mathbb N_0} p_n \gt f(x) – \epsilon\). For \(\delta > 0\) such that the interval \((x-\delta,x)\) doesn’t contain any point of \(\mathbb N_0\) we have for \(y \in (x-\delta,x)\) \[
f(x) – \epsilon \le f(y) = \sum_{d_n \le y} p_n \lt f(x)\] as \(\mathbb N_0 \subset \{n \in \mathbb N \ ; \ d_n \le y\} \subset \mathbb N(x)\). This allows to conclude that \(f\) is continuous at \(x\).