The purpose of this article is to provide some basic counterexamples on real series. Counterexamples are provided as answers to questions.
Unless otherwise stated, (un)n∈N and (vn)n∈N are two real sequences.
If (un) is non-increasing and converges to zero then ∑un converges?
Is not true. A famous counterexample is the harmonic series ∑1n which doesn’t converge as 2p∑k=p+11k≥2p∑k=p+112p=1/2, for all p∈N.
If un=o(1/n) then ∑un converges?
Does not hold as can be seen considering un=1nlnn for n≥2. Indeed ∫x2dttlnt=ln(lnx)–ln(ln2) and therefore ∫∞2dttlnt diverges. We conclude that ∑1nlnn diverges using the integral test. However nun=1lnn converges to zero.
If un=o(vn) and ∑vn converges then ∑un converges?
Is not true as we can see taking vn=(−1)nn and un=1nlnn. ∑vn converges according to the alternating series test and ∑un diverges according to previous paragraph. However limn→∞|unvn|=limn→∞1lnn=0.
If ∑un is a positive converging series then un+1un is bounded?
Not either. Have a look at un={1n2for n even12nfor n odd. Then for p∈N u2p+1u2p=22p+14p2 diverges to ∞. However ∑un converges as ∑1n2 and ∑12n both converge.

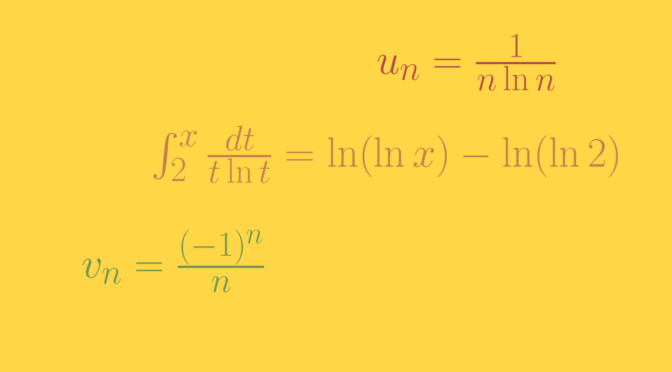
One thought on “Counterexamples around series (part 1)”