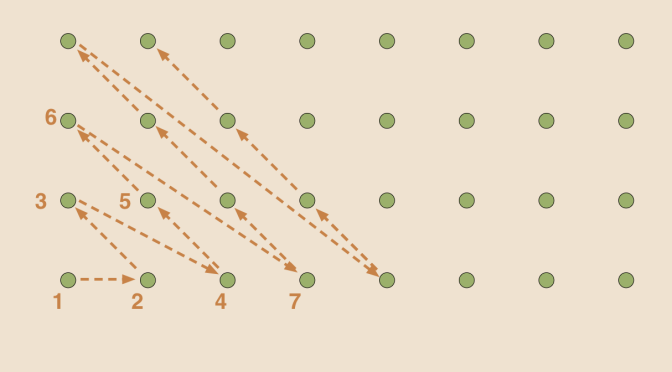
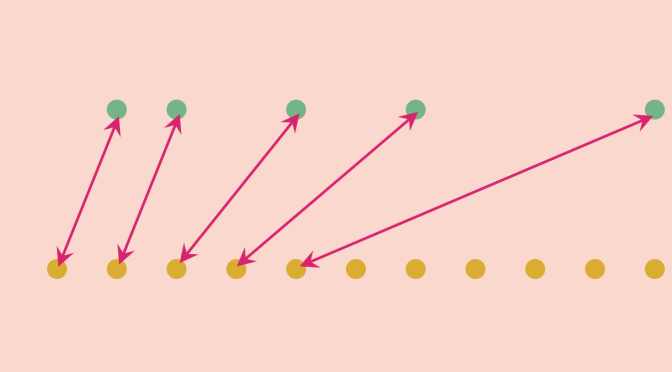
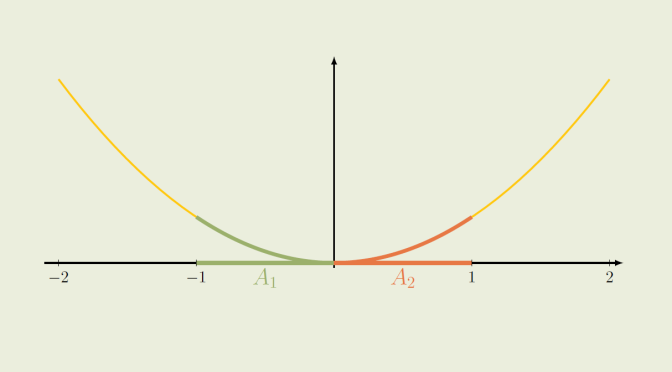
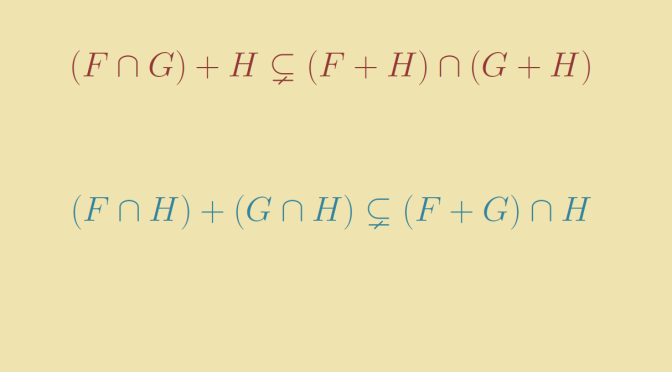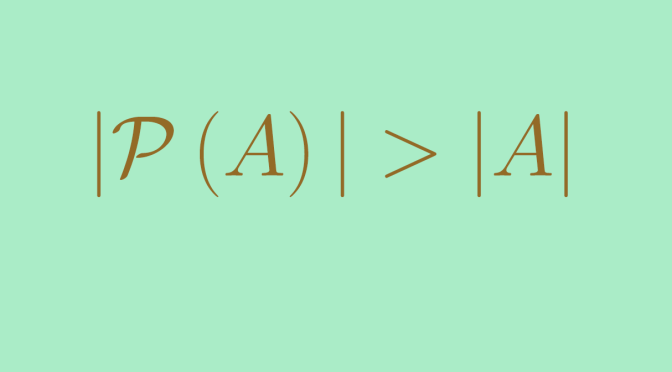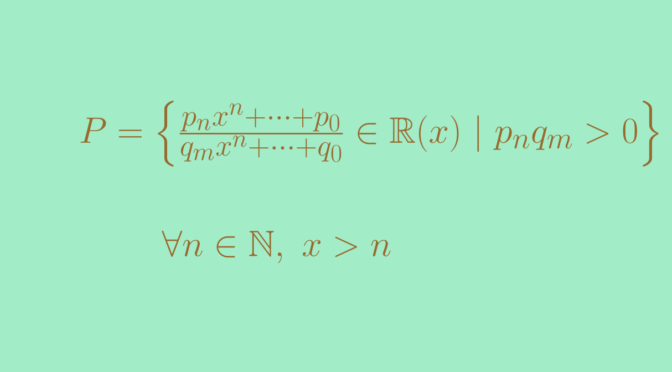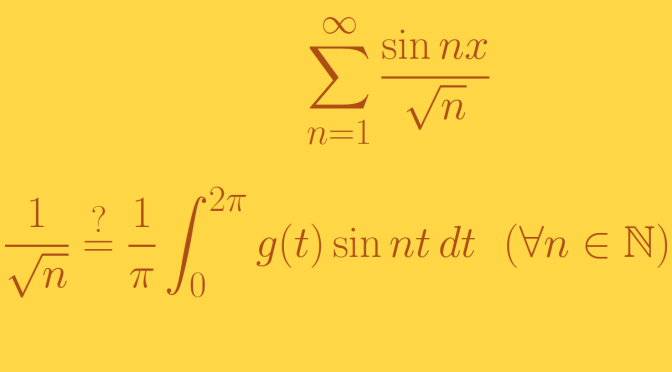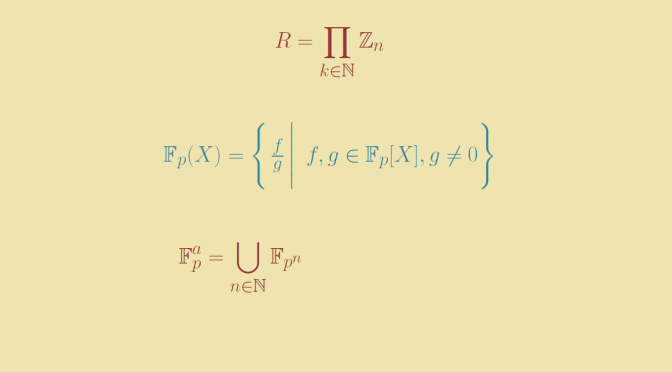All posts by Jean-Pierre Merx

Algebra

Intersection and sum of vector subspaces

Leave a comment

Let’s consider a vector space \(E\) over a field \(K\). We’ll look at relations involving basic set operations and sum of subspaces. We denote by \(F, G\) and \(H\) subspaces of \(E\).

The relation \((F \cap G) + H \subset (F+H) \cap (G + H)\)

This relation holds. The proof is quite simple. For any \(x \in (F \cap G) + H\) there exists \(y \in F \cap G\) and \(h \in H\) such that \(x=y+h\). As \(y \in F\), \(x \in F+H\) and by a similar argument \(x \in F+H\). Therefore \(x \in (F+H) \cap (G + H)\).

Is the inclusion \((F \cap G) + H \subset (F+H) \cap (G + H)\) always an equality? The answer is negative. Take for the space \(E\) the real 3 dimensional space \(\mathbb R^3\). And for the subspaces:

  • \(H\) the plane of equation \(z=0\),
  • \(F\) the line of equations \(y = 0, \, x=z\),
  • \(G\) the line of equations \(y = 0, \, x=-z\),

Continue reading Intersection and sum of vector subspaces →

Analysis

Playing with liminf and limsup

Leave a comment

Let’s consider real sequences \((a_n)_{n \in \mathbb N}\) and \((b_n)_{n \in \mathbb N}\). We look at inequalities involving limit superior and limit inferior of those sequences. Following inequalities hold:
\[\begin{aligned}
& \liminf a_n + \liminf b_n \le \liminf (a_n+b_n)\\
& \liminf (a_n+b_n) \le \liminf a_n + \limsup b_n\\
& \liminf a_n + \limsup b_n \le \limsup (a_n+b_n)\\
& \limsup (a_n+b_n) \le \limsup a_n + \limsup b_n
\end{aligned}\] Let’s prove for example the first inequality, reminding first that \[
\liminf\limits_{n \to \infty} a_n = \lim\limits_{n \to \infty} \left(\inf\limits_{m \ge n} a_m \right).\] For \(n \in \mathbb N\), we have for all \(m \ge n\) \[\inf\limits_{k \ge n} a_k + \inf\limits_{k \ge n} b_k \le a_m + b_m\] hence \[\inf\limits_{k \ge n} a_k + \inf\limits_{k \ge n} b_k \le \inf\limits_{k \ge n} \left(a_k+b_k \right)\] As the sequences \((\inf\limits_{k \ge n} a_k)_{n \in \mathbb N}\) and \((\inf\limits_{k \ge n} b_k)_{n \in \mathbb N}\) are non-increasing we get for all \(n \in \mathbb N\), \[\liminf a_n + \liminf b_n \le \inf\limits_{m \ge n} \left(a_m+b_m \right)\] which leads finally to the desired inequality \[\liminf a_n + \liminf b_n \le \liminf (a_n+b_n).\] Continue reading Playing with liminf and limsup →

Set Theory

There is no greatest cardinal

Leave a comment

We have seen in this article several sets that are infinite and countable. Namely, the set of natural numbers \(\mathbb N\), the set of integers \(\mathbb Z\), the set of rational numbers \(\mathbb Q\). We have seen that the product \(\mathbb N \times \mathbb N\) is also countable. The question then arises, “Are all infinite sets countable?”.

The answer is negative and we prove that \(\mathbb R\) is not countable.

The set of all reals \(\mathbb R\) is not countable

Suppose for the sake of contradiction that \(\mathbb R\) is countable and that \(\mathbb R = \{x_n \ | \ n \in \mathbb N\}\), the \(x_n\) being all distinct. We build by induction two sequences \((a_n)_{n \in \mathbb N}\) increasing and \((b_n)_{n \in \mathbb N}\) decreasing such that:

  • \(a_n < b_n\) for all \(n \in \mathbb N\),
  • \(\vert a_n – b_n \vert \) converges to zero,
  • and \(x_n \notin [a_{n+1},b_{n+1}]\).

Continue reading There is no greatest cardinal →

Set Theory

Counterexamples around cardinality (part 2)

3 Comments

I follow on here from the initial article on cardinality. In that article, we have seen that \(\mathbb N\) contains an infinite countable subset whose complement is also infinite. Namely the subsets of even and odd integers.

Let’s now consider the set \(\mathbb N \times \mathbb N\). \(\mathbb N \times \mathbb N\) contains a countable infinite number of copies of \(\mathbb N\), as for all \(i \in \mathbb N\), \(\{i\} \times \mathbb N \subset \mathbb N \times \mathbb N\). Surprisingly, it is however possible to define a bijection between \(\mathbb N \times \mathbb N\) and \(\mathbb N\).

\(\mathbb N \times \mathbb N\) is equinumerous to \(\mathbb N\)

Consider the map \[\begin{array}{l|rcl}
\varphi : & \mathbb N \times \mathbb N & \longrightarrow & \mathbb N\\
& (n,m) & \longmapsto & 2^{n-1} (2m-1) \end{array}\] \(\varphi\) is one-to-one. Suppose that \(2^{n_1-1} (2m_1-1) = 2^{n_2-1} (2m_2-1)\). If \(n_1=1\), we must also have \(n_2=1\) as \(2 m_1 – 1\) is odd. That implies \((n_1,m_1)=(n_2,m_2)\). Let’s now suppose \(n_1 >1\). According to Euclid’s lemma, \(2^{n_1-1}\) divides \(2^{n_2-1}\) as \(2^{n_1-1}\) is even and \(2m_2 – 1\) odd. By symmetry \(2^{n_2-1}\) also divides \(2^{n_1-1}\). Finally, \(2^{n_1 – 1} = 2^{n_2 – 1}\), \(n_1 = n_2\) and consequently \(m_1 = m_2\). Continue reading Counterexamples around cardinality (part 2) →

Algebra

A non Archimedean ordered field

1 Comment

Let’s recall that an ordered field \(K\) is said to be Archimedean if for any \(a,b \in K\) such that \(0 \lt a \lt b\) it exists a natural number \(n\) such that \(na > b\).

The ordered fields \(\mathbb Q\) or \(\mathbb R\) are Archimedean. We introduce here the example of an ordered field which is not Archimedean. Let’s consider the field of rational functions
\[\mathbb R(x) = \left\{\frac{S(x)}{T(x)} \ | \ S, T \in \mathbb R[x] \right\}\] For \(f(x)=\frac{S(x)}{T(x)} \in \mathbb R(x)\) we can suppose that the polynomials have a constant polynomial greatest common divisor.

Now we define \(P\) as the set of elements \(f(x)=\frac{S(x)}{T(x)} \in \mathbb R(x)\) in which the leading coefficients of \(S\) and \(T\) have the same sign.

One can verify that the subset \(P \subset \mathbb R(x)\) satisfies following two conditions:

ORD 1
Given \(f(x) \in \mathbb R(x)\), we have either \(f(x) \in P\), or \(f(x)=0\), or \(-f(x) \in P\), and these three possibilities are mutually exclusive. In other words, \(\mathbb R(x)\) is the disjoint union of \(P\), \(\{0\}\) and \(-P\).
ORD 2
For \(f(x),g(x) \in P\), \(f(x)+g(x)\) and \(f(x)g(x)\) belong to \(P\).

This means that \(P\) is a positive cone of \(\mathbb R(x)\). Hence, \(\mathbb R(x)\) is ordered by the relation
\[f(x) > 0 \Leftrightarrow f(x) \in P.\]

Now let’s consider the rational fraction \(h(x)=\frac{x}{1} \in \mathbb R(x)\). \(h(x)\) is a positive element, i.e. belongs to \(P\) as \(h-1 = \frac{x-1}{1}\). For any \(n \in \mathbb N\), we have
\[h – n 1=\frac{x-n}{1} \in P\] as the leading coefficients of \(x-n\) and \(1\) are both equal to \(1\). Therefore, we have \(h \gt n 1\) for all \(n \in \mathbb N\), proving that \(\mathbb R(x)\) is not Archimedean.

Analysis

A trigonometric series that is not a Fourier series (Riemann-integration)

1 Comment

We’re looking here at convergent trigonometric series like \[f(x) = a_0 + \sum_{k=1}^\infty (a_n \cos nx + b_n \sin nx)\] which are convergent but are not Fourier series. Which means that the terms \(a_n\) and \(b_n\) cannot be written\[
\begin{array}{ll}
a_n = \frac{1}{\pi} \int_0^{2 \pi} g(t) \cos nt \, dt & (n= 0, 1, \dots) \\
b_n = \frac{1}{\pi} \int_0^{2 \pi} g(t) \sin nt \, dt & (n= 1, 2, \dots)
\end{array}\] where \(g\) is any integrable function.

This raises the question of the type of integral used. We cover here an example based on Riemann integral. I’ll cover a Lebesgue integral example later on.

We prove here that the function \[
f(x)= \sum_{n=1}^\infty \frac{\sin nx}{\sqrt{n}}\] is a convergent trigonometric series but is not a Fourier series. Continue reading A trigonometric series that is not a Fourier series (Riemann-integration) →

Set Theory

Counterexamples around cardinality (part 1)

1 Comment

In mathematics, the cardinality of a set is a measure of the “number of elements of the set”. We denote by \(|A|\) the cardinality of the set \(A\). We say that \(A\) and \(B\) have the same cardinality if there exists a bijection from \(A\) onto \(B\). Such sets said to be equinumerous.

The finite sets satisfy the property that if \(A \subset B\) and \(A\) and \(B\) have the same cardinality then \(A=B\). For example take \(A=\{2,5,42\}\). If \(A \subset B\) and \(B\) has more elements than \(A\), a bijection \(f\) from \(A\) to \(B\) cannot exist as an element in \(B \setminus \{f(2),f(5),f(42)\}\) won’t have an inverse image under \(f\).

This becomes false for infinite sets. Let’s give some examples.

Proper subsets of \(\mathbb N\) equinumerous to \(\mathbb N\)

The set \(A\) of the positive even integers is strictly included in \(\mathbb N\): there exist odd positive integers! However, \(A\) is equinumerous to \(\mathbb N\). The map \(f : n \to 2n\) is a bijection from \(A\) onto \(\mathbb N\).

For our second example, consider the set \(\mathbb P\) of prime numbers. We recall that \(\mathbb P\) is infinite. The proof is quite simple by contradiction. Suppose that there is only a finite number \(\{p_1, \dots, p_n\}\) of prime numbers and consider the number \(N = p_1 p_2 \cdots p_n + 1\). As a consequence of the fundamental theorem of arithmetic, a prime \(q\) divides \(N\). However \(q \notin \{p_1, \dots, p_n\}\) as this would imply \(q\) divides \(1\). From there, we can define by induction a bijection from \(\mathbb N\) onto \(\mathbb P\) by defining \[f(n)=\begin{cases}
2 & \text{for } n=1\\
\min (\mathbb P \setminus \{p_1, \dots, p_n\}) & \text{else }
\end{cases}\] Continue reading Counterexamples around cardinality (part 1) →

Algebra

Infinite rings and fields with positive characteristic

Leave a comment

Familiar to us are infinite fields whose characteristic is equal to zero like \(\mathbb Z, \mathbb Q, \mathbb R\) or the field of constructible numbers.

We’re also familiar with rings having infinite number of elements and zero for characteristic like:

  • The rings of polynomials \(\mathbb Z[X], \mathbb Q[X], \mathbb R[X]\).
  • The rings of matrices \(\mathcal{M}_2(\mathbb R)\).
  • Or the ring of real continuous functions defined on \(\mathbb R\).

We also know rings or fields like integers modulo \(n\) (with \(n \ge 2\)) \(\mathbb Z_n\) or the finite field \(\mathbb F_q\) with \(q=p^r\) elements where \(p\) is a prime.

We provide below examples of infinite rings or fields with positive characteristic.

Infinite rings with positive characteristic

Consider the ring \(\mathbb Z_n[X]\) of polynomials in one variable \(X\) with coefficients in \(\mathbb Z_n\) for \(n \ge 2\) integer. It is an infinite ring since \(\mathbb X^m \in \mathbb{Z}_n[X]\) for all positive integers \(m\), and \(X^r \neq X^s\) for \(r \neq s\). But the characteristic of \(\mathbb Z_n[X]\) is clearly \(n\).

Another example is based on product of rings. If \(I\) is an index set and \((R_i)_{i \in I}\) a family of rings, one can define the product ring \(\displaystyle \prod_{i \in I} R_i\). The operations are defined the natural way with \((a_i)_{i \in I} + (b_i)_{i \in I} = (a_i+b_i)_{i \in I}\) and \((a_i)_{i \in I} \cdot (b_i)_{i \in I} = (a_i \cdot b_i)_{i \in I}\). Fixing \(n \ge 2\) integer and taking \(I = \mathbb N\), \(R_i = \mathbb Z_n\) for all \(i \in I\) we get the ring \(\displaystyle R = \prod_{k \in \mathbb N} \mathbb Z_n\). \(R\) multiplicative identity is the sequence with all terms equal to \(1\). The characteristic of \(R\) is \(n\) and \(R\) is obviously infinite. Continue reading Infinite rings and fields with positive characteristic →

Set Theory

Playing with images and inverse images

Leave a comment

We’re looking here to relational expressions involving image and inverse image.

We consider a function \(f : X \to Y\) from the set \(X\) to the set \(Y\). If \(x\) is a member of \(X\), \(f(x)\) is the image of \(x\) under \(f\).
The image of a subset \(A \subset X\) under \(f\) is the subset (of \(Y\)) \[f(A)\stackrel{def}{=} \{f(x) : x \in A\}.\]

The inverse image of a subset \(B \subset Y\) is the subset of \(A\) \[f^{-1}(B)\stackrel{def}{=} \{x \in X : f(x) \in B\}.\] Important to understand is that here, \(f^{-1}\) is not the inverse function of \(f\).

We now look at relational expressions involving the image and the inverse image under \(f\).

Inverse images with unions and intersections

Following relations hold:
\[\begin{array}{c}
f^{-1}(B_1 \cup B_2) = f^{-1}(B_1) \cup f^{-1}(B_2)\\
f^{-1}(B_1 \cap B_2) = f^{-1}(B_1) \cap f^{-1}(B_2)
\end{array}\] Let’s prove the first equality as an example. We have \(x \in f^{-1}(B_1 \cup B_2)\) if and only if \(f(x) \in B_1 \cup B_2\) if and only if \(f(x) \in B_1\) or \(f(x) \in B_2\) which means exactly \(x \in f^{-1}(B_1) \cup f^{-1}(B_2)\). Continue reading Playing with images and inverse images →

Topology

Counterexamples around balls in metric spaces

Leave a comment

Let’s play with balls in a metric space \((M,d)\). We denote by

  • \(B_r(p) = \{x \in M : d(x,p) < r\}\) the open ball.
  • \(B_r[p] = \{x \in M : d(x,p) \le r\}\) the closed ball.

A ball of radius \(r\) included in a ball of radius \(r^\prime < r\)

We take for \(M\) the space \(\{0\} \cup [2, \infty)\) equipped with the standard metric distance \(d(x,y)=\vert x – y \vert\).

We have \(B_4(0) = \{0\} \cup [2, 4)\) while \(B_3(2) = \{0\} \cup [2, 5)\). Despite having a strictly smaller radius, the ball \(B_3(2)\) strictly contains the ball \(B_4(0)\).

The phenomenon cannot happen in a normed vector space \((M, \Vert \cdot \Vert)\). For the proof, take two open balls \(B_r(p),B_{r^\prime}(p^\prime) \subset M\), \(0 < r^\prime < r\) and suppose that \(p \in B_{r^\prime}(p^\prime)\). If \(p=p^\prime\) and \(q \in B_{r^\prime}(p^\prime) \setminus \{p^\prime\}\) then \(p + \frac{\frac{r+r^\prime}{2} }{\Vert p q \Vert} p q \in B_r(p) \setminus B_{r^\prime}(p^\prime) \). And if \(p \neq p^\prime\), \(p \in B_{r^\prime}(p^\prime)\) then \(p^\prime + \frac{\frac{r+r^\prime}{2} }{\Vert p^\prime p \Vert} p^\prime p \in B_r(p) \setminus B_{r^\prime}(p^\prime) \).

An open ball \(B_r(p)\) whose closure is not equal to the closed ball \(B_r[p]\)

Here we take for \(M\) a subspace of \(\mathbb R^2\) which is the union of the origin \(\{0\}\) with the unit circle \(S^1\). For the distance, we use the Euclidean norm.
The open unit ball centered at the origin \(B_1(0)\) is reduced to the origin: \(B_1(0) = \{0\}\). Its closure \(\overline{B_1(0)}\) is itself. However the closed ball \(B_1[0]\) is the all space \(\{0\} \cup S^1\).

Again one can prove that for a normed vector space this cannot happen. The closure of an open ball is the closed ball for a normed vector space.