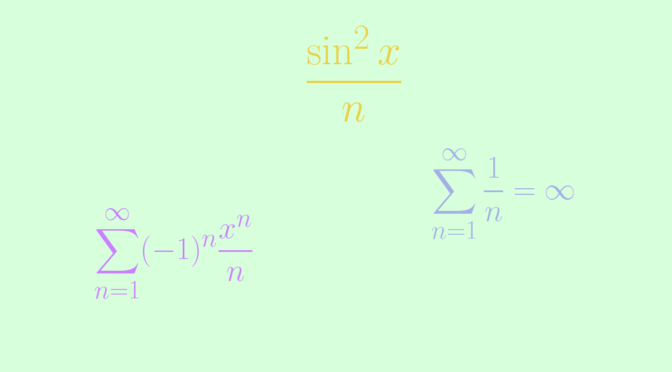All posts by Jean-Pierre Merx

Analysis

A uniformly but not normally convergent function series

Leave a comment

Consider a functions series \(\displaystyle \sum f_n\) of functions defined on a set \(S\) to \(\mathbb R\) or \(\mathbb C\). It is known that if \(\displaystyle \sum f_n\) is normally convergent, then \(\displaystyle \sum f_n\) is uniformly convergent.

The converse is not true and we provide two counterexamples.

Consider first the sequence of functions \((g_n)\) defined on \(\mathbb R\) by:
\[g_n(x) = \begin{cases}
\frac{\sin^2 x}{n} & \text{for } x \in (n \pi, (n+1) \pi)\\
0 & \text{else}
\end{cases}\] The series \(\displaystyle \sum \Vert g_n \Vert_\infty\) diverges as for all \(n \in \mathbb N\), \(\Vert g_n \Vert_\infty = \frac{1}{n}\) and the harmonic series \(\sum \frac{1}{n}\) diverges. However the series \(\displaystyle \sum g_n\) converges uniformly as for \(x \in \mathbb R\) the sum \(\displaystyle \sum g_n(x)\) is having only one term and \[
\vert R_n(x) \vert = \left\vert \sum_{k=n+1}^\infty g_k(x) \right\vert \le \frac{1}{n+1}\]

For our second example, we consider the sequence of functions \((f_n)\) defined on \([0,1]\) by \(f_n(x) = (-1)^n \frac{x^n}{n}\). For \(x \in [0,1]\) \(\displaystyle \sum (-1)^n \frac{x^n}{n}\) is an alternating series whose absolute value of the terms converge to \(0\) monotonically. According to Leibniz test, \(\displaystyle \sum (-1)^n \frac{x^n}{n}\) is well defined and we can apply the classical inequality \[
\displaystyle \left\vert \sum_{k=1}^\infty (-1)^k \frac{x^k}{k} – \sum_{k=1}^m (-1)^k \frac{x^k}{k} \right\vert \le \frac{x^{m+1}}{m+1} \le \frac{1}{m+1}\] for \(m \ge 1\). Which proves that \(\displaystyle \sum (-1)^n \frac{x^n}{n}\) converges uniformly on \([0,1]\).

However the convergence is not normal as \(\sup\limits_{x \in [0,1]} \frac{x^n}{n} = \frac{1}{n}\).

Analysis

Root test

Leave a comment

The root test is a test for the convergence of a series \[
\sum_{n=1}^\infty a_n \] where each term is a real or complex number. The root test was developed first by Augustin-Louis Cauchy.

We denote \[l = \limsup\limits_{n \to \infty} \sqrt[n]{\vert a_n \vert}.\] \(l\) is a non-negative real number or is possibly equal to \(\infty\). The root test states that:

  • if \(l < 1\) then the series converges absolutely;
  • if \(l > 1\) then the series diverges.

The root test is inconclusive when \(l = 1\).

A case where \(l=1\) and the series diverges

The harmonic series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n}\) is divergent. However \[\sqrt[n]{\frac{1}{n}} = \frac{1}{n^{\frac{1}{n}}}=e^{- \frac{1}{n} \ln n} \] and \(\limsup\limits_{n \to \infty} \sqrt[n]{\frac{1}{n}} = 1\) as \(\lim\limits_{n \to \infty} \frac{\ln n}{n} = 0\).

A case where \(l=1\) and the series converges

Consider the series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}\). We have \[\sqrt[n]{\frac{1}{n^2}} = \frac{1}{n^{\frac{2}{n}}}=e^{- \frac{2}{n} \ln n} \] Therefore \(\limsup\limits_{n \to \infty} \sqrt[n]{\frac{1}{n^2}} = 1\), while the series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}\) is convergent as we have seen in the ratio test article. Continue reading Root test →

Analysis

Ratio test

1 Comment

The ratio test is a test for the convergence of a series \[
\sum_{n=1}^\infty a_n \] where each term is a real or complex number and is nonzero when \(n\) is large. The test is sometimes known as d’Alembert’s ratio test.

Suppose that \[\lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert = l\] The ratio test states that:

  • if \(l < 1\) then the series converges absolutely;
  • if \(l > 1\) then the series diverges.

What if \(l = 1\)? One cannot conclude in that case.

Cases where \(l=1\) and the series diverges

Consider the harmonic series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n}\). We have \(\lim\limits_{n \to \infty} \frac{n+1}{n} = 1\). It is well know that the harmonic series diverges. Recall that one proof uses the Cauchy’s convergence test based for \(k \ge 1\) on the inequalities: \[
\sum_{n=2^k+1}^{2^{k+1}} \frac{1}{n} \ge \sum_{n=2^k+1}^{2^{k+1}} \frac{1}{2^{k+1}} = \frac{2^{k+1}-2^k}{2^{k+1}} \ge \frac{1}{2}\]

An even simpler case is the series \(\displaystyle \sum_{n=1}^\infty 1\).

Cases where \(l=1\) and the series converges

We also have \(\lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert = 1\) for the infinite series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}\). The series is however convergent as for \(n \ge 1\) we have:\[
0 \le \frac{1}{(n+1)^2} \le \frac{1}{n(n+1)} = \frac{1}{n} – \frac{1}{n+1}\] and the series \(\displaystyle \sum_{n=1}^\infty \left(\frac{1}{n} – \frac{1}{n+1} \right)\) obviously converges.

Another example is the alternating series \(\displaystyle \sum_{n=1}^\infty \frac{(-1)^n}{n}\).

Algebra

A simple ring which is not a division ring

Leave a comment

Let’s recall that a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. A division ring is a simple ring. Is the converse true? The answer is negative and we provide here a counterexample of a simple ring which is not a division ring.

We prove that for \(n \ge 1\) the matrix ring \(M_n(F)\) of \(n \times n\) matrices over a field \(F\) is simple. \(M_n(F)\) is obviously not a division ring as the matrix with \(1\) at position \((1,1)\) and \(0\) elsewhere is not invertible.

Let’s prove first following lemma. Continue reading A simple ring which is not a division ring →

Set Theory

Small open sets containing the rationals

Leave a comment

The set \(\mathbb Q\) of the rational number is countable infinite and dense in \(\mathbb R\). You can have a look here on a way to build a bijective map between \(\mathbb N\) and \(\mathbb Q\).

Now given \(\epsilon > 0\), can one find an open set \(O_\epsilon\) of measure less than \(\epsilon\) with \(\mathbb Q \subseteq O_\epsilon\)?

The answer is positive. Let’s denote \[
O_\epsilon = \bigcup_{n \in \mathbb N} (r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\] where \((r_n)_{n \in \mathbb N}\) is an enumeration of the rationals. Obviously \(\mathbb Q \subseteq O_\epsilon\). Using countable subadditivity of Lebesgue measure \(\mu\), we get:
\begin{align*}
\mu(O_\epsilon) &\le \sum_{n \in \mathbb N} \mu((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}}))\\
&= \sum_{n \in \mathbb N} \frac{2 \epsilon}{2^{n+1}} = \sum_{n \in \mathbb N} \frac{\epsilon}{2^n} = \epsilon
\end{align*}

Therefore we’re done. Some additional comments:

  • While Lebesgue measure of the reals is infinite and the rationals are dense in the reals, we can include the rationals in an open set of measure as small as desired!
  • The open segments \((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\) are overlapping. Hence \(\mu(O_\epsilon)\) is strictly less than \(\epsilon\).
Analysis

A continuous function with divergent Fourier series

1 Comment

It is known that for a piecewise continuously differentiable function \(f\), the Fourier series of \(f\) converges at all \(x \in \mathbb R\) to \(\frac{f(x^-)+f(x^+)}{2}\).

We describe Fejér example of a continuous function with divergent Fourier series. Fejér example is the even, \((2 \pi)\)-periodic function \(f\) defined on \([0,\pi]\) by: \[
f(x) = \sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\]
According to Weierstrass M-test, \(f\) is continuous. We denote \(f\) Fourier series by \[
\frac{1}{2} a_0 + (a_1 \cos x + b_1 \sin x) + \dots + (a_n \cos nx + b_n \sin nx) + \dots.\]

As \(f\) is even, the \(b_n\) are all vanishing. If we denote for all \(m \in \mathbb N\):\[
\lambda_{n,m}=\int_0^{\pi} \sin \left[ (2m + 1) \frac{t}{2} \right] \cos nt \ dt \text{ and } \sigma_{n,m} = \sum_{k=0}^n \lambda_{k,m},\]
we have:\[
\begin{aligned}
a_n &=\frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \cos nt \ dt= \frac{2}{\pi} \int_0^{\pi} f(t) \cos nt \ dt\\
&= \frac{2}{\pi} \int_0^{\pi} \left(\sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\right) \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \int_0^{\pi} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right] \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \lambda_{n,2^{p^3-1}}
\end{aligned}\] One can switch the \(\int\) and \(\sum\) signs as the series is normally convergent.

We now introduce for all \(n \in \mathbb N\):\[
S_n = \frac{\pi}{2} \sum_{k=0}^n a_k = \sum_{p=1}^\infty \sum_{k=0}^n \frac{1}{p^2} \lambda_{k,2^{p^3-1}}
=\sum_{p=1}^\infty \frac{1}{p^2} \sigma_{n,2^{p^3-1}}\]

We will prove below that for all \(n,m \in \mathbb N\) we have \(\sigma_{m,m} \ge \frac{1}{2} \ln m\) and \(\sigma_{n,m} \ge 0\). Assuming those inequalities for now, we get:\[
S_{2^{p^3-1}} \ge \frac{1}{p^2} \sigma_{2^{p^3-1},2^{p^3-1}} \ge \frac{1}{2p^2} \ln(2^{p^3-1}) = \frac{p^3-1}{2p^2} \ln 2\]
As the right hand side diverges to \(\infty\), we can conclude that \((S_n)\) diverges and consequently that the Fourier series of \(f\) diverges at \(0\). Continue reading A continuous function with divergent Fourier series →

Analysis

Radius of convergence of power series

Leave a comment

We look here at the radius of convergence of the sum and product of power series.

Let’s recall that for a power series \(\displaystyle \sum_{n=0}^\infty a_n x^n\) where \(0\) is not the only convergence point, the radius of convergence is the unique real \(0 < R \le \infty\) such that the series converges whenever \(\vert x \vert < R\) and diverges whenever \(\vert x \vert > R\).

Given two power series with radii of convergence \(R_1\) and \(R_2\), i.e.
\begin{align*}
\displaystyle f_1(x) = \sum_{n=0}^\infty a_n x^n, \ \vert x \vert < R_1 \\ \displaystyle f_2(x) = \sum_{n=0}^\infty b_n x^n, \ \vert x \vert < R_2 \end{align*} The sum of the power series \begin{align*} \displaystyle f_1(x) + f_2(x) &= \sum_{n=0}^\infty a_n x^n + \sum_{n=0}^\infty b_n x^n \\ &=\sum_{n=0}^\infty (a_n + b_n) x^n \end{align*} and its Cauchy product:
\begin{align*}
\displaystyle f_1(x) \cdot f_2(x) &= \left(\sum_{n=0}^\infty a_n x^n\right) \cdot \left(\sum_{n=0}^\infty b_n x^n \right) \\
&=\sum_{n=0}^\infty \left( \sum_{l=0}^n a_l b_{n-l}\right) x^n
\end{align*}
both have radii of convergence greater than or equal to \(\min \{R_1,R_2\}\).

The radii can indeed be greater than \(\min \{R_1,R_2\}\). Let’s give examples.
Continue reading Radius of convergence of power series →

Set Theory

A partially ordered set having multiple minimal elements

Leave a comment

Let’s consider a partially ordered set (or poset) \(E\).

If \(E\) is totally ordered, \(E\) has at most one minimal element. If \(E\) is not totally ordered, \(E\) can have multiple minimal elements. We provide an example for the set \(E=\{n \in \mathbb N \ | \ n \ge 2\}\). For two natural numbers \(n\) and \(m\), we write \(n|m\) if \(n\) divides \(m\). One easily sees that this yields a partial order.

The minimal elements of \(E\) are the elements not having divisors, this is the case for all prime numbers \(p \in E\).

\(E\) has an infinite number of minimal elements which are the prime numbers.

Algebra

Unique factorization domain that is not a Principal ideal domain

Leave a comment

In this article, we provide an example of a unique factorization domain – UFD that is not a principal ideal domain – PID. However, it is known that a PID is a UFD.

We take a field \(F\), for example \(\mathbb Q\), \(\mathbb R\), \(\mathbb F_p\) (where \(p\) is a prime) or whatever more exotic.

The polynomial ring \(F[X]\) is a UFD. This follows from the fact that \(F[X]\) is a Euclidean domain. It is also known that for a UFD \(R\), \(R[X]\) is also a UFD. Therefore the polynomial ring \(F[X_1,X_2]\) in two variables is a UFD as \(F[X_1,X_2] = F[X_1][X_2]\). However the ideal \(I=(X_1,X_2)\) is not principal. Let’s prove it by contradiction.

Suppose that \((X_1,X_2) = (P)\) with \(P \in F[X_1,X_2]\). Then there exist two polynomials \(Q_1,Q_2 \in F[X_1,X_2]\) such that \(X_1=PQ_1\) and \(X_2=PQ_2\). As a polynomial in variable \(X_2\), the polynomial \(X_1\) is having degree \(0\). Therefore, the degree of \(P\) as a polynomial in variable \(X_2\) is also equal to \(0\). By symmetry, we get that the degree of \(P\) as a polynomial in variable \(X_1\) is equal to \(0\) too. Which implies that \(P\) is an element of the field \(F\) and consequently that \((X_1,X_2) = F[X_1,X_2]\).

But the equality \((X_1,X_2) = F[X_1,X_2]\) is absurd. Indeed, the degree of a polynomial \(X_1 T_1 + X_2 T_2\) cannot be equal to \(0\) for any \(T_1,T_2 \in F[X_1,X_2]\). And therefore \(1 \notin F[X_1,X_2]\).