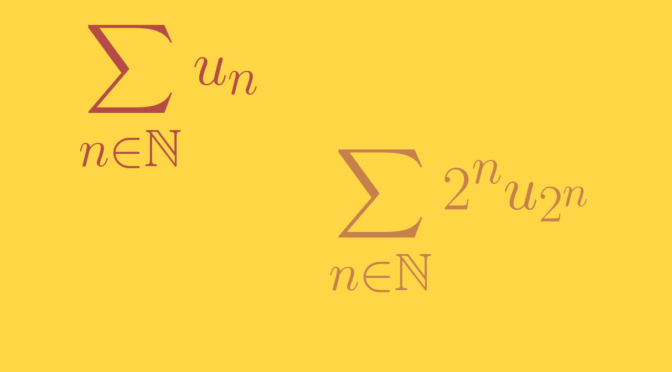All posts by Jean-Pierre Merx

Analysis

Counterexamples around Cauchy condensation test

1 Comment

According to Cauchy condensation test: for a non-negative, non-increasing sequence \((u_n)_{n \in \mathbb N}\) of real numbers, the series \(\sum_{n \in \mathbb N} u_n\) converges if and only if the condensed series \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) converges.

The test doesn’t hold for any non-negative sequence. Let’s have a look at counterexamples.

A sequence such that \(\sum_{n \in \mathbb N} u_n\) converges and \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges

Consider the sequence \[
u_n=\begin{cases}
\frac{1}{n} & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
0 & \text{ else} \end{cases}\] For \(n \in \mathbb N\) we have \[
0 \le \sum_{k = 1}^n u_k \le \sum_{k = 1}^{2^n} u_k = \sum_{k = 1}^{n} \frac{1}{2^k} < 1,\] therefore \(\sum_{n \in \mathbb N} u_n\) converges as its partial sums are positive and bounded above. However \[\sum_{k=1}^n 2^k u_{2^k} = \sum_{k=1}^n 1 = n,\] so \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges.

A sequence such that \(\sum_{n \in \mathbb N} v_n\) diverges and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges

Consider the sequence \[
v_n=\begin{cases}
0 & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
\frac{1}{n} & \text{ else} \end{cases}\] We have \[
\sum_{k = 1}^{2^n} v_k = \sum_{k = 1}^{2^n} \frac{1}{k} – \sum_{k = 1}^{n} \frac{1}{2^k} > \sum_{k = 1}^{2^n} \frac{1}{k} -1\] which proves that the series \(\sum_{n \in \mathbb N} v_n\) diverges as the harmonic series is divergent. However for \(n \in \mathbb N\), \(2^n v_{2^n} = 0 \) and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges.

Analysis

Counterexamples around the Cauchy product of real series

Leave a comment

Let \(\sum_{n = 0}^\infty a_n, \sum_{n = 0}^\infty b_n\) be two series of real numbers. The Cauchy product \(\sum_{n = 0}^\infty c_n\) is the series defined by \[
c_n = \sum_{k=0}^n a_k b_{n-k}\] According to the theorem of Mertens, if \(\sum_{n = 0}^\infty a_n\) converges to \(A\), \(\sum_{n = 0}^\infty b_n\) converges to \(B\) and at least one of the two series is absolutely convergent, their Cauchy product converges to \(AB\). This can be summarized by the equality \[
\left( \sum_{n = 0}^\infty a_n \right) \left( \sum_{n = 0}^\infty b_n \right) = \sum_{n = 0}^\infty c_n\]

The assumption stating that at least one of the two series converges absolutely cannot be dropped as shown by the example \[
\sum_{n = 0}^\infty a_n = \sum_{n = 0}^\infty b_n = \sum_{n = 0}^\infty \frac{(-1)^n}{\sqrt{n+1}}\] Those series converge according to Leibniz test, as the sequence \((1/\sqrt{n+1})\) decreases monotonically to zero. However, the Cauchy product is defined by \[
c_n=\sum_{k=0}^n \frac{(-1)^k}{\sqrt{k+1}} \cdot \frac{(-1)^{n-k}}{\sqrt{n-k+1}} = (-1)^n \sum_{k=0}^n \frac{1}{\sqrt{(k+1)(n-k+1)}}\] As we have \(1 \le k+ 1 \le n+1\) and \(1 \le n-k+ 1 \le n+1\) for \(k = 0 \dots n\), we get \(\frac{1}{\sqrt{(k+1)(n-k+1)}} \ge \frac{1}{n+1}\) and therefore \(\vert c_n \vert \ge 1\) proving that the Cauchy product of \(\sum_{n = 0}^\infty a_n\) and \(\sum_{n = 0}^\infty b_n\) diverges.

The Cauchy product may also converge while the initial series both diverge. Let’s consider \[
\begin{cases}
(a_n) = (2, 2, 2^2, \dots, 2^n, \dots)\\
(b_n) = (-1, 1, 1, 1, \dots)
\end{cases}\] The series \(\sum_{n = 0}^\infty a_n, \sum_{n = 0}^\infty b_n\) diverge. Their Cauchy product is the series defined by \[
c_n=\begin{cases}
-2 & \text{ for } n=0\\
0 & \text{ for } n>0
\end{cases}\] which is convergent.

Analysis

A linear differential equation with no solution to an initial value problem

Leave a comment


Consider a first order linear differential equation \[
y^\prime(x) = A(x)y(x) + B(x)\] where \(A, B\) are real continuous functions defined on a non-empty real interval \(I\). According to Picard-Lindelöf theorem, the initial value problem \[
\begin{cases}
y^\prime(x) = A(x)y(x) + B(x)\\
y(x_0) = y_0, \ x_0 \in I
\end{cases}\] has a unique solution defined on \(I\).

However, a linear differential equation \[
c(x)y^\prime(x) = A(x)y(x) + B(x)\] where \(A, B, c\) are real continuous functions might not have a solution to an initial value problem. Let’s have a look at the equation \[
x y^\prime(x) = y(x) \tag{E}\label{eq:IVP}\] for \(x \in \mathbb R\). The equation is linear.

For \(x \in (-\infty,0)\) a solution to \eqref{eq:IVP} is a solution of the explicit differential linear equation \[
y^\prime(x) = \frac{y(x)}x\] hence can be written \(y(x) = \lambda_-x\) with \(\lambda_- \in \mathbb R\). Similarly, a solution to \eqref{eq:IVP} on the interval \((0,\infty)\) is of the form \(y(x) = \lambda_+ x\) with \(\lambda_+ \in \mathbb R\).

A global solution to \eqref{eq:IVP}, i.e. defined on the whole real line is differentiable at \(0\) hence the equation \[
\lambda_- = y_-^\prime(0)=y_+^\prime(0) = \lambda_+\] which means that \(y(x) = \lambda x\) where \(\lambda=\lambda_-=\lambda_+\).

In particular all solutions defined on \(\mathbb R\) are such that \(y(0)=0\). Therefore the initial value problem \[
\begin{cases}
x y^\prime(x) = y(x)\\
y(0)=1
\end{cases}\] has no solution.

Algebra

Field not algebraic over an intersection but algebraic over each initial field

Leave a comment

Let’s describe an example of a field \(K\) which is of degree \(2\) over two distinct subfields \(M\) and \(N\) respectively, but not algebraic over \(M \cap N\).

Let \(K=F(x)\) be the rational function field over a field \(F\) of characteristic \(0\), \(M=F(x^2)\) and \(N=F(x^2+x)\). I claim that those fields provide the example we’re looking for.

\(K\) is of degree \(2\) over \(M\) and \(N\)

The polynomial \(\mu_M(t)=t^2-x^2\) belongs to \(M[t]\) and \(x \in K\) is a root of \(\mu_M\). Also, \(\mu_M\) is irreducible over \(M=F(x^2)\). If that wasn’t the case, \(\mu_M\) would have a root in \(F(x^2)\) and there would exist two polynomials \(p,q \in F[t]\) such that \[
p^2(x^2) = x^2 q^2(x^2)\] which cannot be, as can be seen considering the degrees of the polynomials of left and right hand sides. This proves that \([K:M]=2\). Considering the polynomial \(\mu_N(t)=t^2-t-(x^2+x)\), one can prove that we also have \([K:N]=2\).

We have \(M \cap N=F\)

The mapping \(\sigma_M : x \mapsto -x\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(M\) are fixed under \(\sigma_M\). Similarly, the mapping \(\sigma_N : x \mapsto -x-1\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(N\) are fixed under \(\sigma_N\). Also \[
(\sigma_N\circ\sigma_M)(x)=\sigma_N(\sigma_M(x))=\sigma_N(-x)=-(-x-1)=x+1.\] An element \(z=p(x)/q(x) \in M \cap N\) where \(p(x),q(x)\) are coprime polynomials of \(K=F(x)\) is fixed under \(\sigma_M \circ \sigma_N\). Therefore following equality holds \[
\frac{p(x)}{q(x)}=z=(\sigma_2\circ\sigma_1)(z)=\frac{p(x+1)}{q(x+1)},\] which is equivalent to \[
p(x)q(x+1)=p(x+1)q(x).\] By induction, we get for \(n \in \mathbb Z\) \[
p(x)q(x+n)=p(x+n)q(x).\] Assume \(p(x)\) is not a constant polynomial. Then it has a root \(\alpha\) in some finite extension \(E\) of \(F\). As \(p(x),q(x)\) are coprime polynomials, \(q(\alpha) \neq 0\). Consequently \(p(\alpha+n)=0\) for all \(n \in \mathbb Z\) and the elements \(\alpha +n\) are all distinct as the characteristic of \(F\) is supposed to be non zero. This implies that \(p(x)\) is the zero polynomial, in contradiction with our assumption. Therefore \(p(x)\) is a constant polynomial and \(q(x)\) also according to a similar proof. Hence \(z\) is constant as was supposed to be proven.

Finally, \(K=F(x)\) is not algebraic over \(F=M \cap N\) as \((1,x, x^2, \dots, x^n, \dots)\) is independent over the field \(F\) which concludes our claims on \(K, M\) and \(N\).

Analysis

Pointwise convergence not uniform on any interval

Leave a comment

We provide in this article an example of a pointwise convergent sequence of real functions that doesn’t converge uniformly on any interval.

Let’s consider a sequence \((a_p)_{p \in \mathbb N}\) enumerating the set \(\mathbb Q\) of rational numbers. Such a sequence exists as \(\mathbb Q\) is countable.

Now let \((g_n)_{n \in \mathbb N}\) be the sequence of real functions defined on \(\mathbb R\) by \[
g_n(x) = \sum_{p=1}^{\infty} \frac{1}{2^p} f_n(x-a_p)\] where \(f_n : x \mapsto \frac{n^2 x^2}{1+n^4 x^4}\) for \(n \in \mathbb N\).

\(f_n\) main properties

\(f_n\) is a rational function whose denominator doesn’t vanish. Hence \(f_n\) is indefinitely differentiable. As \(f_n\) is an even function, we can study it only on \([0,\infty)\).

We have \[
f_n^\prime(x)= 2n^2x \frac{1-n^4x^4}{(1+n^4 x^4)^2}.\] \(f_n^\prime\) vanishes at zero (like \(f_n\)) is positive on \((0,\frac{1}{n})\), vanishes at \(\frac{1}{n}\) and is negative on \((\frac{1}{n},\infty)\). Hence \(f_n\) has a maximum at \(\frac{1}{n}\) with \(f_n(\frac{1}{n}) = \frac{1}{2}\) and \(0 \le f_n(x) \le \frac{1}{2}\) for all \(x \in \mathbb R\).

Also for \(x \neq 0\) \[
0 \le f_n(x) =\frac{n^2 x^2}{1+n^4 x^4} \le \frac{n^2 x^2}{n^4 x^4} = \frac{1}{n^2 x^2}\] consequently \[
0 \le f_n(x) \le \frac{1}{n} \text{ for } x \ge \frac{1}{\sqrt{n}}.\]

\((g_n)\) converges pointwise to zero

First, one can notice that \(g_n\) is well defined. For \(x \in \mathbb R\) and \(p \in \mathbb N\) we have \(0 \le \frac{1}{2^p} f_n(x-a_p) \le \frac{1}{2^p} \cdot\ \frac{1}{2}=\frac{1}{2^{p+1}}\) according to previous paragraph. Therefore the series of functions \(\sum \frac{1}{2^p} f_n(x-a_p)\) is normally convergent. \(g_n\) is also continuous as for all \(p \in \mathbb N\) \(x \mapsto \frac{1}{2^p} f_n(x-a_p)\) is continuous. Continue reading Pointwise convergence not uniform on any interval →

Algebra

Complex matrix without a square root

Leave a comment

Consider for \(n \ge 2\) the linear space \(\mathcal M_n(\mathbb C)\) of complex matrices of dimension \(n \times n\). Is a matrix \(T \in \mathcal M_n(\mathbb C)\) always having a square root \(S \in \mathcal M_n(\mathbb C)\), i.e. a matrix such that \(S^2=T\)? is the question we deal with.

First, one can note that if \(T\) is similar to \(V\) with \(T = P^{-1} V P\) and \(V\) has a square root \(U\) then \(T\) also has a square root as \(V=U^2\) implies \(T=\left(P^{-1} U P\right)^2\).

Diagonalizable matrices

Suppose that \(T\) is similar to a diagonal matrix \[
D=\begin{bmatrix}
d_1 & 0 & \dots & 0 \\
0 & d_2 & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n
\end{bmatrix}\] Any complex number has two square roots, except \(0\) which has only one. Therefore, each \(d_i\) has at least one square root \(d_i^\prime\) and the matrix \[
D^\prime=\begin{bmatrix}
d_1^\prime & 0 & \dots & 0 \\
0 & d_2^\prime & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n^\prime
\end{bmatrix}\] is a square root of \(D\). Continue reading Complex matrix without a square root →

Topology

Intersection and union of interiors

Leave a comment

Consider a topological space \(E\). For subsets \(A, B \subseteq E\) we have the equality \[
A^\circ \cap B^\circ = (A \cap B)^\circ\] and the inclusion \[
A^\circ \cup B^\circ \subseteq (A \cup B)^\circ\] where \(A^\circ\) and \(B^\circ\) denote the interiors of \(A\) and \(B\).

Let’s prove that \(A^\circ \cap B^\circ = (A \cap B)^\circ\).

We have \(A^\circ \subseteq A\) and \(B^\circ \subseteq B\) and therefore \(A^\circ \cap B^\circ \subseteq A \cap B\). As \(A^\circ \cap B^\circ\) is open we then have \(A^\circ \cap B^\circ \subseteq (A \cap B)^\circ\) because \(A^\circ \cap B^\circ\) is open and \((A \cap B)^\circ\) is the largest open subset of \(A \cap B\).

Conversely, \(A \cap B \subseteq A\) implies \((A \cap B)^\circ \subseteq A^\circ\) and similarly \((A \cap B)^\circ \subseteq B^\circ\). Therefore we have \((A \cap B)^\circ \subseteq A^\circ \cap B^\circ\) which concludes the proof of the equality \(A^\circ \cap B^\circ = (A \cap B)^\circ\).

One can also prove the inclusion \(A^\circ \cup B^\circ \subseteq (A \cup B)^\circ\). However, the equality \(A^\circ \cup B^\circ = (A \cup B)^\circ\) doesn’t always hold. Let’s provide a couple of counterexamples.

For the first one, let’s take for \(E\) the plane \(\mathbb R^2\) endowed with usual topology. For \(A\), we take the unit close disk and for \(B\) the plane minus the open unit disk. \(A^\circ\) is the unit open disk and \(B^\circ\) the plane minus the unit closed disk. Therefore \(A^\circ \cup B^\circ = \mathbb R^2 \setminus C\) is equal to the plane minus the unit circle \(C\). While we have \[A \cup B = (A \cup B)^\circ = \mathbb R^2.\]

For our second counterexample, we take \(E=\mathbb R\) endowed with usual topology and \(A = \mathbb R \setminus \mathbb Q\), \(B = \mathbb Q\). Here we have \(A^\circ = B^\circ = \emptyset\) thus \(A^\circ \cup B^\circ = \emptyset\) while \(A \cup B = (A \cup B)^\circ = \mathbb R\).

The union of the interiors of two subsets is not always equal to the interior of the union.

Algebra

Additive subgroups of vector spaces

Leave a comment

Consider a vector space \(V\) over a field \(F\). A subspace \(W \subseteq V\) is an additive subgroup of \((V,+)\). The converse might not be true.

If the characteristic of the field is zero, then a subgroup \(W\) of \(V\) might not be an additive subgroup. For example \(\mathbb R\) is a vector space over \(\mathbb R\) itself. \(\mathbb Q\) is an additive subgroup of \(\mathbb R\). However \(\sqrt{2}= \sqrt{2}.1 \notin \mathbb Q\) proving that \(\mathbb Q\) is not a subspace of \(\mathbb R\).

Another example is \(\mathbb Q\) which is a vector space over itself. \(\mathbb Z\) is an additive subgroup of \(\mathbb Q\), which is not a subspace as \(\frac{1}{2} \notin \mathbb Z\).

Yet, an additive subgroup of a vector space over a prime field \(\mathbb F_p\) with \(p\) prime is a subspace. To prove it, consider an additive subgroup \(W\) of \((V,+)\) and \(x \in W\). For \(\lambda \in F\), we can write \(\lambda = \underbrace{1 + \dots + 1}_{\lambda \text{ times}}\). Consequently \[
\lambda \cdot x = (1 + \dots + 1) \cdot x= \underbrace{x + \dots + x}_{\lambda \text{ times}} \in W.\]

Finally an additive subgroup of a vector space over any finite field is not always a subspace. For a counterexample, take the non-prime finite field \(\mathbb F_{p^2}\) (also named \(\text{GF}(p^2)\)). \(\mathbb F_{p^2}\) is also a vector space over itself. The prime finite field \(\mathbb F_p \subset \mathbb F_{p^2}\) is an additive subgroup that is not a subspace of \(\mathbb F_{p^2}\).

Analysis

A differentiable real function with unbounded derivative around zero

Leave a comment

Consider the real function defined on \(\mathbb R\)\[
f(x)=\begin{cases}
0 &\text{for } x = 0\\
x^2 \sin \frac{1}{x^2} &\text{for } x \neq 0
\end{cases}\]

\(f\) is continuous and differentiable on \(\mathbb R\setminus \{0\}\). For \(x \in \mathbb R\) we have \(\vert f(x) \vert \le x^2\), which implies that \(f\) is continuous at \(0\). Also \[
\left\vert \frac{f(x)-f(0)}{x} \right\vert = \left\vert x \sin \frac{1}{x^2} \right\vert \le \vert x \vert\] proving that \(f\) is differentiable at zero with \(f^\prime(0) = 0\). The derivative of \(f\) for \(x \neq 0\) is \[
f^\prime(x) = \underbrace{2x \sin \frac{1}{x^2}}_{=g(x)}-\underbrace{\frac{2}{x} \cos \frac{1}{x^2}}_{=h(x)}\] On the interval \((-1,1)\), \(g(x)\) is bounded by \(2\). However, for \(a_k=\frac{1}{\sqrt{k \pi}}\) with \(k \in \mathbb N\) we have \(h(a_k)=2 \sqrt{k \pi} (-1)^k\) which is unbounded while \(\lim\limits_{k \to \infty} a_k = 0\). Therefore \(f^\prime\) is unbounded in all neighborhood of the origin.

Analysis

A Riemann-integrable map that is not regulated

Leave a comment

For a Banach space \(X\), a function \(f : [a,b] \to X\) is said to be regulated if there exists a sequence of step functions \(\varphi_n : [a,b] \to X\) converging uniformly to \(f\).

One can prove that a regulated function \(f : [a,b] \to X\) is Riemann-integrable. Is the converse true? The answer is negative and we provide below an example of a Riemann-integrable real function that is not regulated. Let’s first prove following theorem.

THEOREM A bounded function \(f : [a,b] \to \mathbb R\) that is (Riemann) integrable on all intervals \([c, b]\) with \(a < c < b\) is integrable on \([a,b]\).

PROOF Take \(M > 0\) such that for all \(x \in [a,b]\) we have \(\vert f(x) \vert < M\). For \(\epsilon > 0\), denote \(c = \inf(a + \frac{\epsilon}{4M},b + \frac{b-a}{2})\). As \(f\) is supposed to be integrable on \([c,b]\), one can find a partition \(P\): \(c=x_1 < x_2 < \dots < x_n =b\) such that \(0 \le U(f,P) - L(f,P) < \frac{\epsilon}{2}\) where \(L(f,P),U(f,P)\) are the lower and upper Darboux sums. For the partition \(P^\prime\): \(a= x_0 < c=x_1 < x_2 < \dots < x_n =b\), we have \[ \begin{aligned} 0 \le U(f,P^\prime) - L(f,P^\prime) &\le 2M(c-a) + \left(U(f,P) - L(f,P)\right)\\ &< 2M \frac{\epsilon}{4M} + \frac{\epsilon}{2} = \epsilon \end{aligned}\] We now prove that the function \(f : [0,1] \to [0,1]\) defined by \[ f(x)=\begin{cases} 1 &\text{ if } x \in \{2^{-k} \ ; \ k \in \mathbb N\}\\ 0 &\text{otherwise} \end{cases}\] is Riemann-integrable (that follows from above theorem) and not regulated. Let's prove it. If \(f\) was regulated, there would exist a step function \(g\) such that \(\vert f(x)-g(x) \vert < \frac{1}{3}\) for all \(x \in [0,1]\). If \(0=x_0 < x_1 < \dots < x_n=1\) is a partition associated to \(g\) and \(c_1\) the value of \(g\) on the interval \((0,x_1)\), we must have \(\vert 1-c_1 \vert < \frac{1}{3}\) as \(f\) takes (an infinite number of times) the value \(1\) on \((0,x_1)\). But \(f\) also takes (an infinite number of times) the value \(0\) on \((0,x_1)\). Hence we must have \(\vert c_1 \vert < \frac{1}{3}\). We get a contradiction as those two inequalities are not compatible.