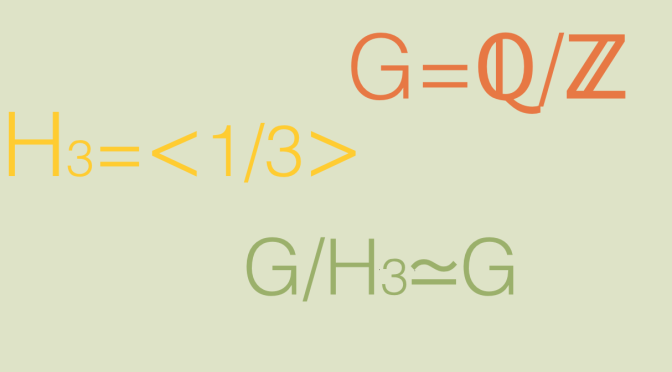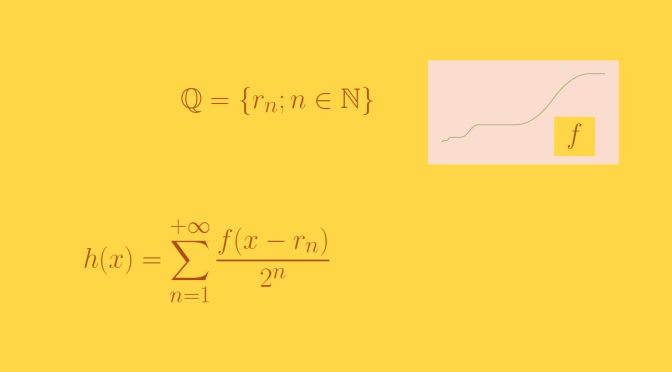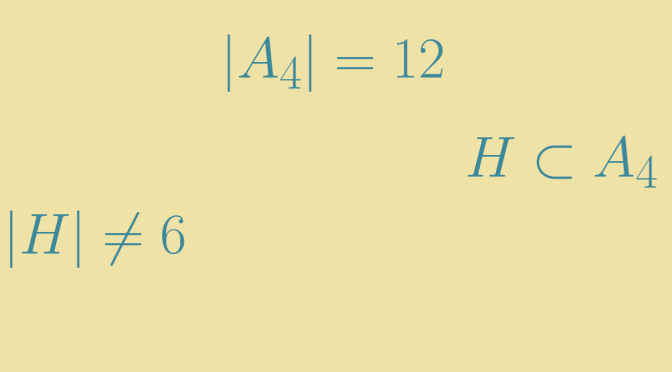All posts by Jean-Pierre Merx

Topology

Continuous maps that are not closed or not open

Leave a comment

We recall some definitions on open and closed maps. In topology an open map is a function between two topological spaces which maps open sets to open sets. Likewise, a closed map is a function which maps closed sets to closed sets.

For a continuous function \(f: X \mapsto Y\), the preimage \(f^{-1}(V)\) of every open set \(V \subseteq Y\) is an open set which is equivalent to the condition that the preimages of the closed sets (which are the complements of the open subsets) in \(Y\) are closed in \(X\). However, a continuous function might not be an open map or a closed map as we prove in following counterexamples. Continue reading Continuous maps that are not closed or not open →

Algebra

A finitely generated soluble group isomorphic to a proper quotient group

Leave a comment

Let \(\mathbb{Q}_2\) be the ring of rational numbers of the form \(m2^n\) with \(m, n \in \mathbb{Z}\) and \(N = U(3, \mathbb{Q}_2)\) the group of unitriangular matrices of dimension \(3\) over \(\mathbb{Q}_2\). Let \(t\) be the diagonal matrix with diagonal entries: \(1, 2, 1\) and put \(H = \langle t, N \rangle\). We will prove that \(H\) is finitely generated and that one of its quotient group \(G\) is isomorphic to a proper quotient group of \(G\). Continue reading A finitely generated soluble group isomorphic to a proper quotient group →

Algebra

A (not finitely generated) group isomorphic to a proper quotient group

Leave a comment

The basic question that we raise here is the following one: given a group \(G\) and a proper subgroup \(H\) (i.e. \(H \notin \{\{1\},G\}\), can \(G/H\) be isomorphic to \(G\)? A group \(G\) is said to be hopfian (after Heinz Hopf) if it is not isomorphic with a proper quotient group.

All finite groups are hopfian as \(|G/H| = |G| \div |H|\). Also, all simple groups are hopfian as a simple group doesn’t have proper subgroups.

So we need to turn ourselves to infinite groups to uncover non hopfian groups. Continue reading A (not finitely generated) group isomorphic to a proper quotient group →

Analysis

A continuous function not differentiable at the rationals but differentiable elsewhere

Leave a comment

We build here a continuous function of one real variable whose derivative exists on \(\mathbb{R} \setminus \mathbb{Q}\) and doesn’t have a left or right derivative on each point of \(\mathbb{Q}\).

As \(\mathbb{Q}\) is (infinitely) countable, we can find a bijection \(n \mapsto r_n\) from \(\mathbb{N}\) to \(\mathbb{Q}\). We now reuse the function \(f\) defined here. Recall \(f\) main properties: Continue reading A continuous function not differentiable at the rationals but differentiable elsewhere →

Analysis

A differentiable function except at one point with a bounded derivative

1 Comment

We build here a continuous function of one real variable whose derivative exists except at \(0\) and is bounded on \(\mathbb{R^*}\).

We start with the even and piecewise linear function \(g\) defined on \([0,+\infty)\) with following values:
\[g(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x =0\\
0 & \mbox{if } x \in \{\frac{k}{4^n};(k,n) \in \{1,2,4\} \times \mathbb{N^*}\}\\
1 & \mbox{if } x \in \{\frac{3}{4^n};n \in \mathbb{N^*}\}\\
\end{array}
\right.
\]
The picture below gives an idea of the graph of \(g\) for positive values. Continue reading A differentiable function except at one point with a bounded derivative →

Algebra

Converse of Lagrange’s theorem does not hold

Leave a comment

Lagrange’s theorem, states that for any finite group \(G\), the order (number of elements) of every subgroup \(H\) of \(G\) divides the order of \(G\) (denoted by \(\vert G \vert\)).

Lagrange’s theorem raises the converse question as to whether every divisor \(d\) of the order of a group is the order of some subgroup. According to Cauchy’s theorem this is true when \(d\) is a prime.

However, this does not hold in general: given a finite group \(G\) and a divisor \(d\) of \(\vert G \vert\), there does not necessarily exist a subgroup of \(G\) with order \(d\). The alternating group \(G = A_4\), which has \(12\) elements has no subgroup of order \(6\). We prove it below. Continue reading Converse of Lagrange’s theorem does not hold →

Analysis

A continuous function which is not of bounded variation

Leave a comment

Introduction on total variation of functions

Recall that a function of bounded variation, also known as a BV-function, is a real-valued function whose total variation is bounded (finite).

Being more formal, the total variation of a real-valued function \(f\), defined on an interval \([a,b] \subset \mathbb{R}\) is the quantity:
\[V_a^b(f) = \sup\limits_{P \in \mathcal{P}} \sum_{i=0}^{n_P-1} \left\vert f(x_{i+1}) – f(x_i) \right\vert\] where the supremum is taken over the set \(\mathcal{P}\) of all partitions of the interval considered. Continue reading A continuous function which is not of bounded variation →

Topology

A curve filling a square – Lebesgue example

Leave a comment

Introduction

We aim at defining a continuous function \(\varphi : [0,1] \rightarrow [0,1]^2\). At first sight this looks quite strange.

Indeed, \(\varphi\) cannot be a bijection. If \(\varphi\) would be bijective, it would also be an homeomorphism as a continuous bijective function from a compact space to a Haussdorff space is an homeomorphism. But an homeomorphism preserves connectedness and \([0,1] \setminus \{1/2\}\) is not connected while \([0,1]^2 \setminus \{\varphi(1/2)\}\) is.

Nor can \(\varphi\) be piecewise continuously differentiable as the Lebesgue measure of \(\varphi([0,1])\) would be equal to \(0\).

\(\varphi\) is defined in two steps using the Cantor space \(K\). Continue reading A curve filling a square – Lebesgue example →