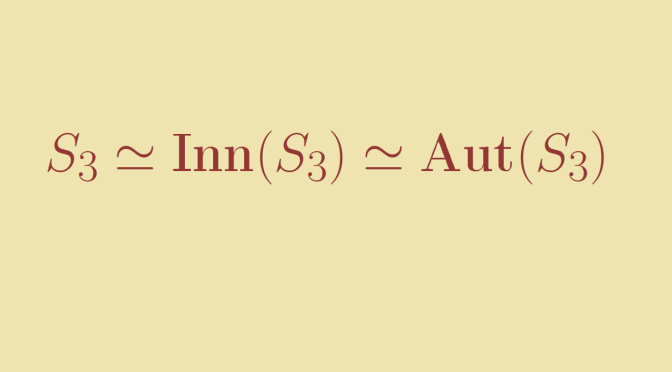All posts by Jean-Pierre Merx

Algebra

A group isomorphic to its automorphism group

Leave a comment

We consider a group \(G\) and we look at its automorphism group \(\text{Aut}(G)\). Can \(G\) be isomorphic to
\(\text{Aut}(G)\)? The answer is positive and we’ll prove that it is the case for the symmetric group \(S_3\).

Consider the morphism \[
\begin{array}{l|rcl}
\Phi : & S_3 & \longrightarrow & \text{Aut}(S_3) \\
& a & \longmapsto & \varphi_a \end{array}\]
where \(\varphi_a\) is the inner automorphism \(\varphi_a : x \mapsto a^{-1}xa\). It is easy to verify that \(\Phi\) is indeed a group morphism. The kernel of \(\Phi\) is the center of \(S_3\) which is having the identity for only element. Hence \(\Phi\) is one-to-one and \(S_3 \simeq \Phi(S_3)\). Therefore it is sufficient to prove that \(\Phi\) is onto. As \(|S_3|=6\), we’ll be finished if we prove that \(|\text{Aut}(S_3)|=6\).

Generally, for \(G_1,G_2\) groups and \(f : G_1 \to G_2\) a one-to-one group morphism, the image of an element \(x\) of order \(k\) is an element \(f(x)\) having the same order \(k\). So for \(\varphi \in \text{Aut}(S_3)\) the image of a transposition is a transposition. As the transpositions \(\{(1 \ 2), (1 \ 3), (2 \ 3)\}\) generate \((S_3)\), \(\varphi\) is completely defined by \(\{\varphi((1 \ 2)), \varphi((1 \ 3)), \varphi((2 \ 3))\}\). We have 3 choices to define the image of \((1 \ 2)\) under \(\varphi\) and then 2 choices for the image of \((1 \ 3)\) under \(\varphi\). The image of \((2 \ 3)\) under \(\varphi\) is the remaining transposition.

Finally, we have proven that \(|\text{Aut}(S_3)|=6\) as desired and \(S_3 \simeq \text{Aut}(S_3)\).

Topology

Playing with interior and closure

Leave a comment

Let’s play with the closure and the interior of sets.

To start the play, we consider a topological space \(E\) and denote for any subspace \(A \subset E\): \(\overline{A}\) the closure of \(A\) and \(\overset{\circ}{A}\) the interior of \(A\).

Warm up with the closure operator

For \(A,B\) subsets of \(E\), the following results hold: \(\overline{\overline{A}}=\overline{A}\), \(A \subset B \Rightarrow \overline{A} \subset \overline{B}\), \(\overline{A \cup B} = \overline{A} \cup \overline{B}\) and \(\overline{A \cap B} \subset \overline{A} \cap \overline{B}\).

Let’s prove it.
\(\overline{A}\) being closed, it is equal to its closure and \(\overline{\overline{A}}=\overline{A}\).

Suppose that \(A \subset B\). As \(B \subset \overline{B}\), we have \(A \subset \overline{B}\). Also, \(\overline{B}\) is closed so it contains \(\overline{A}\), which proves \(\overline{A} \subset \overline{B}\).

Let’s consider \(A,B \in E\) two subsets. As \(A \subset A \cup B\), we have \(\overline{A} \subset \overline{A \cup B}\) and similarly \(\overline{B} \subset \overline{A \cup B}\). Hence \(\overline{A} \cup \overline{B} \subset \overline{A \cup B}\). Conversely, \(A \cup B \subset \overline{A} \cup \overline{B}\) and \(\overline{A} \cup \overline{B}\) is closed. So \(\overline{A \cup B} \subset \overline{A} \cup \overline{B}\) and finally \(\overline{A \cup B} = \overline{A} \cup \overline{B}\).

Regarding the inclusion \(\overline{A \cap B} \subset \overline{A} \cap \overline{B}\), we notice that \(A \cap B \subset \overline{A} \cap \overline{B}\) and that \(\overline{A} \cap \overline{B}\) is closed to get the conclusion.

However, the implication \(\overline{A} \subset \overline{B} \Rightarrow A \subset B\) doesn’t hold. For a counterexample, consider the space \(E=\mathbb R\) equipped with the topology induced by the absolute value distance and take \(A=[0,1)\), \(B=(0,1]\). We have \(\overline{A}=\overline{B}=[0,1]\).

The equality \(\overline{A} \cap \overline{B} = \overline{A \cap B}\) doesn’t hold as well. For the proof, just consider \(A=[0,1)\) and \(B=(1,2]\). Continue reading Playing with interior and closure →

Analysis

A discontinuous real convex function

Leave a comment

Consider a function \(f\) defined on a real interval \(I \subset \mathbb R\). \(f\) is called convex if: \[\forall x, y \in I \ \forall \lambda \in [0,1]: \ f((1-\lambda)x+\lambda y) \le (1-\lambda) f(x) + \lambda f(y)\]

Suppose that \(I\) is a closed interval: \(I=[a,b]\) with \(a < b\). For \(a < s < t < u < b\) one can prove that: \[\frac{f(t)-f(s)}{t-s}\le \frac{f(u)-f(s)}{u-s}\le\frac{f(u)-f(t)}{u-t}.\] It follows from those relations that \(f\) has left-hand and right-hand derivatives at each point of the interior of \(I\). And therefore that \(f\) is continuous at each point of the interior of \(I\).
Is a convex function defined on an interval \(I\) continuous at all points of the interval? That might not be the case and a simple example is the function: \[\begin{array}{l|rcl}
f : & [0,1] & \longrightarrow & \mathbb R \\
& x & \longmapsto & 0 \text{ for } x \in (0,1) \\
& x & \longmapsto & 1 \text{ else}\end{array}\]

It can be easily verified that \(f\) is convex. However, \(f\) is not continuous at \(0\) and \(1\).

Algebra

Is the quotient group of a finite group always isomorphic to a subgroup?

Leave a comment

Given a normal subgroup \(H\) of a finite group \(G\), is \(G/H\) always isomorphic to a subgroup \(K \le G\)?

The case of an abelian group

According to the fundamental theorem of finite abelian groups, every finite abelian group \(G\) can be expressed as the direct sum of cyclic subgroups of prime-power order: \[G \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\alpha_i}}\] where \(p_1, \dots , p_u\) are primes and \(\alpha_1, \dots , \alpha_u\) non zero integers.

If \(H \le G\) we have \[H \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\beta_i}}\] with \(0 \le \beta_1 \le \alpha_1, \dots, 0 \le \beta_u \le \alpha_u\). Then \[G/H \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\alpha_i-\beta_i}}\] which is a subgroup of \(G\).

If \(G\) is not abelian, then \(G/H\) might not be isomorphic to a subgroup of \(G\). Continue reading Is the quotient group of a finite group always isomorphic to a subgroup? →

Topology

Counterexamples to Banach fixed-point theorem

Leave a comment

Let \((X,d)\) be a metric space. Then a map \(T : X \to X\) is called a contraction map if it exists \(0 \le k < 1\) such that \[d(T(x),T(y)) \le k d(x,y)\] for all \(x,y \in X\). According to Banach fixed-point theorem, if \((X,d)\) is a complete metric space and \(T\) a contraction map, then \(T\) admits a fixed-point \(x^* \in X\), i.e. \(T(x^*)=x^*\).

We look here at counterexamples to the Banach fixed-point theorem when some hypothesis are not fulfilled.

First, let’s consider \[\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x+1 \end{array}\] For all \(x,y \in \mathbb R\) we have \(\vert f(x)-f(y) \vert = \vert x- y \vert\). \(f\) is not a contraction, but an isometry. Obviously, \(f\) has no fixed-point.

We now prove that a map satisfying \[d(g(x),g(y)) < d(x,y)\] might also not have a fixed-point. A counterexample is the following map \[\begin{array}{l|rcl} g : & [0,+\infty) & \longrightarrow & [0,+\infty) \\ & x & \longmapsto & \sqrt{1+x^2} \end{array}\] Since \[g^\prime(\xi) = \frac{\xi}{\sqrt{1+\xi^2}} < 1 \text{ for all } \xi \in [0, +\infty),\] by the mean value theorem \[\vert g(x) - g(y)| = \vert g^\prime(\xi)\vert |x-y| < |x-y| \text{ for all } x, y \in [0, +\infty).\] However \(g\) has no fixed-point. Finally, let's have a look to a space \((X,d)\) which is not complete. We take \(a,b \in \mathbb R\) with \(0 < a < 1\) and for \((X,d)\) the space \(X = \mathbb R \setminus \{\frac{b}{1-a}\}\) equipped with absolute value distance. \(X\) is not complete. Consider the map \[\begin{array}{l|rcl} h : & X & \longrightarrow & X \\ & x & \longmapsto & ax + b \end{array}\] \(h\) is well defined as for \(x \neq \frac{b}{1-a}\), \(h(x) \neq \frac{b}{1-a}\). \(h\) is a contraction map as for \(x,y \in \mathbb R\) \[\vert h(x)-h(y) \vert = a \vert x - y \vert \] However, \(h\) doesn't have a fixed-point in \(X\) as \(\frac{b}{1-a}\) is the only real for which \(h(x)=x\).

Analysis

Differentiability of multivariable real functions (part1)

2 Comments

This article provides counterexamples about differentiability of functions of several real variables. We focus on real functions of two real variables (defined on \(\mathbb R^2\)). \(\mathbb R^2\) and \(\mathbb R\) are equipped with their respective Euclidean norms denoted by \(\Vert \cdot \Vert\) and \(\vert \cdot \vert\), i.e. the absolute value for \(\mathbb R\).

We recall some definitions and theorems about differentiability of functions of several real variables.

Definition 1 We say that a function \(f : \mathbb R^2 \to \mathbb R\) is differentiable at \(\mathbf{a} \in \mathbb R^2\) if it exists a (continuous) linear map \(\nabla f(\mathbf{a}) : \mathbb R^2 \to \mathbb R\) with \[\lim\limits_{\mathbf{h} \to 0} \frac{f(\mathbf{a}+\mathbf{h})-f(\mathbf{a})-\nabla f(\mathbf{a}).\mathbf{h}}{\Vert \mathbf{h} \Vert} = 0\]

Definition 2 Let \(f : \mathbb R^n \to \mathbb R\) be a real-valued function. Then the \(\mathbf{i^{th}}\) partial derivative at point \(\mathbf{a}\) is the real number
\begin{align*}
\frac{\partial f}{\partial x_i}(\mathbf{a}) &= \lim\limits_{h \to 0} \frac{f(\mathbf{a}+h \mathbf{e_i})- f(\mathbf{a})}{h}\\
&= \lim\limits_{h \to 0} \frac{f(a_1,\dots,a_{i-1},a_i+h,a_{i+1},\dots,a_n) – f(a_1,\dots,a_{i-1},a_i,a_{i+1},\dots,a_n)}{h}
\end{align*} For two real variable functions, \(\frac{\partial f}{\partial x}(x,y)\) and \(\frac{\partial f}{\partial y}(x,y)\) will denote the partial derivatives.

Definition 3 Let \(f : \mathbb R^n \to \mathbb R\) be a real-valued function. The directional derivative of \(f\) along vector \(\mathbf{v}\) at point \(\mathbf{a}\) is the real \[\nabla_{\mathbf{v}}f(\mathbf{a}) = \lim\limits_{h \to 0} \frac{f(\mathbf{a}+h \mathbf{v})- f(\mathbf{a})}{h}\] Continue reading Differentiability of multivariable real functions (part1) →

Algebra

Two non similar matrices having same minimal and characteristic polynomials

Leave a comment

Consider a square matrix \(A\) of dimension \(n \ge 1\) over a field \(\mathbb F\), i.e. \(A \in \mathcal M_n(\mathbb F)\). Results discuss below are true for any field \(\mathbb F\), in particular for \(\mathbb F = \mathbb R\) or \(\mathbb F = \mathbb C\).

A polynomial \(P \in \mathbb F[X]\) is called a vanishing polynomial for \(A\) if \(P(A) = 0\). If the matrix \(B\) is similar to \(B\) (which means that \(B=Q^{-1} A Q\) for some invertible matrix \(Q\)), and the polynomial \(P\) vanishes at \(A\) then \(P\) also vanishes at \(B\). This is easy to prove as we have \(P(B)=P(Q^{-1} A Q)=Q^{-1} P(A) Q\).

In particular, two similar matrices have the same minimal and characteristic polynomials.

Is the converse true? Are two matrices having the same minimal and characteristic polynomials similar? Continue reading Two non similar matrices having same minimal and characteristic polynomials →

Topology

A counterexample to Krein-Milman theorem

Leave a comment

In the theory of functional analysis, the Krein-Milman theorem states that for a separated locally convex topological vector space \(X\), a compact convex subset \(K\) is the closed convex hull of its extreme points.

For the reminder, an extreme point of a convex set \(S\) is a point in \(S\) which does not lie in any open line segment joining two points of S. A point \(p \in S\) is an extreme point of \(S\) if and only if \(S \setminus \{p\}\) is still convex.

In particular, according to the Krein-Milman theorem, a non-empty compact convex set has a non-empty set of extreme points. Let see what happens if we weaken some hypothesis of Krein-Milman theorem. Continue reading A counterexample to Krein-Milman theorem →

Analysis

Continuity of multivariable real functions

1 Comment

This article provides counterexamples about continuity of functions of several real variables. In addition the article discusses the cases of functions of two real variables (defined on \(\mathbb R^2\) having real values. \(\mathbb R^2\) and \(\mathbb R\) are equipped with their respective Euclidean norms denoted by \(\Vert \cdot \Vert\) and \(\vert \cdot \vert\), i.e. the absolute value for \(\mathbb R\).

We recall that a function \(f\) defined from \(\mathbb R^2\) to \(\mathbb R\) is continuous at \((x_0,y_0) \in \mathbb R^2\) if for any \(\epsilon > 0\), there exists \(\delta > 0\), such that \(\Vert (x,y) -(x_0,y_0) \Vert < \delta \Rightarrow \vert f(x,y) - f(x_0,y_0) \vert < \epsilon\). Continue reading Continuity of multivariable real functions →

Algebra

A simple group whose order is not a prime

Leave a comment

Consider a finite group \(G\) whose order (number of elements) is a prime number. It is well known that \(G\) is cyclic and simple. Which means that \(G\) has no non trivial normal subgroup.

Is the converse true, i.e. are the cyclic groups with prime orders the only simple groups? The answer is negative. We prove here that for \(n \ge 5\) the alternating group \(A_n\) is simple. In particular \(A_5\) whose order is equal to \(60\) is simple. Continue reading A simple group whose order is not a prime →