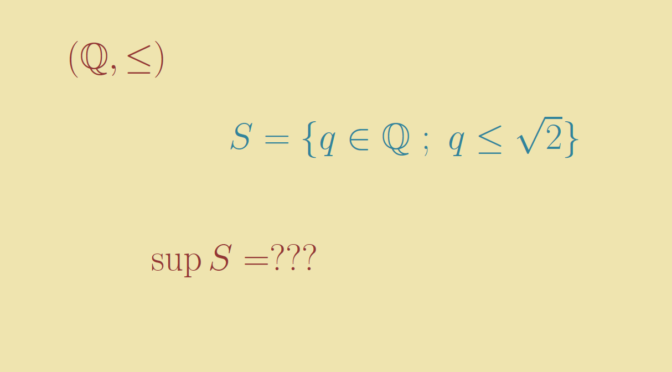Consider a linearly ordered set \((X, \le)\) and a subset \(S \subseteq X\). Let’s recall some definitions:

• \(S\) is bounded above if there exists an element \(k \in X\) such that \(k \ge s\) for all \(s \in S\).
• \(g\) is a greatest element of \(S\) is \(g \in S\) and \(g \ge s\) for all \(s \in S\). \(l\) is a lowest element of \(S\) is \(l \in S\) and \(l \le s\) for all \(s \in S\).
• \(a\) is an supremum of \(S\) if it is the least element in \(X\) that is greater than or equal to all elements of \(S\).

Subsets with a supremum but no greatest element

Let’s give examples of subsets having a supremum but no greatest element. First consider the ordered set \((\mathbb R, \le)\) and the subset \(S=\{ q \in \mathbb Q \ ; \ q \le \sqrt{2}\}\). \(S\) is bounded above by \(2\). \(\sqrt{2}\) is a supremum of \(S\) as we have \(q \le \sqrt{2}\) for all \(q \in S\) and as for \(b < \sqrt{2}\), it exists \(q \in \mathbb Q\) such that \(b < q < \sqrt{2}\) because \(\mathbb Q\) is dense in \(\mathbb R\). However \(S\) doesn't have a greatest element because \(\sqrt{2}\) is an irrational number.

For our second example we take \(X = \mathbb N \times \mathbb N\) ordered lexicographically by \(\preceq\). The subset \(S=\{(0,n) \ ; \ n \in \mathbb N\}\) is bounded above by \((2,0)\). Moreover \((1,0)\) is a supremum. But \(S\) doesn’t have a greatest element as for \((0,n) \in S\) we have \((0,n) \prec (0,n+1)\).

Bounded above subsets with no supremum

Leveraging the examples above, we take \((X, \le) = (\mathbb Q, \le)\) and \(S=\{ q \in \mathbb Q \ ; \ q \le \sqrt{2}\}\). \(S\) is bounded above, by \(2\) for example. However \(S\) doesn’t have a supremum because \(\sqrt{2} \notin \mathbb Q\).

Another example is the set \(X = \mathbb N \times \mathbb Z\) ordered lexicographically by \(\preceq\). The subset \(S=\{(0,n) \ ; \ n \in \mathbb N\}\) is bounded above by \((2,0)\) but has no supremum. Indeed, the elements greater or equal to all the elements of \(S\) are the elements \((a,b)\) with \(a \ge 1\). However \((a,b)\) with \(a \ge 1\) cannot be a supremum of \(S\), as \((a,b-1) \prec (a,b)\) and \((a,b-1)\) is greater than all the elements of \(S\).