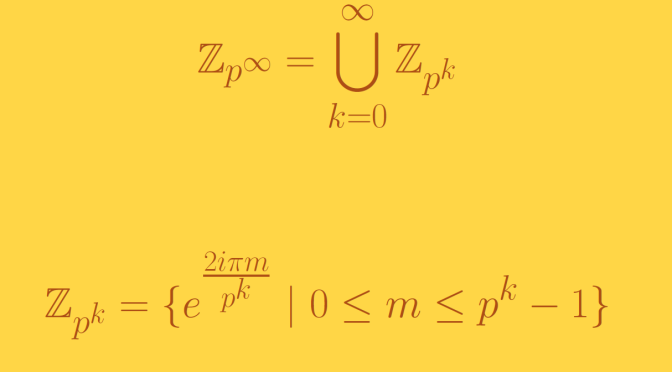We study some properties of the Prüfer $p$-group $\mathbb{Z}_{p^\infty}$ for a prime number $p$. The Prüfer $p$-group may be identified with the subgroup of the circle group, consisting of all $p^n$-th roots of unity as $n$ ranges over all non-negative integers:
$$\mathbb{Z}_{p^\infty}=\bigcup_{k=0}^\infty \mathbb{Z}_{p^k} \text{ where } \mathbb{Z}_{p^k}= \{e^{\frac{2 i \pi m}{p^k}} \ | \ 0 \le m \le p^k-1\}$$

$\mathbb{Z}_{p^\infty}$ is a group

First, let’s notice that for $0 \le m \le n$ integers we have $\mathbb{Z}_{p^m} \subseteq \mathbb{Z}_{p^n}$ as $p^m | p^n$. Also for $m \ge 0$ $\mathbb{Z}_{p^m}$ is a subgroup of the circle group. We also notice that all elements of $\mathbb{Z}_{p^\infty}$ have finite orders which are powers of $p$.

Now for $z_1,z_2$ elements of $\mathbb{Z}_{p^\infty}$, there exist $k_1,k_2 \ge 0$ with $z_1 \in \mathbb{Z}_{p^{k_1}}$ and $z_2 \in \mathbb{Z}_{p^{k_2}}$. We can suppose without loss of generality that $k_1 \le k_2$. Hence $z_1, z_2\ \in \mathbb{Z}_{p^{k_2}}$ and $z_1 z_2^{-1} \in \mathbb{Z}_{p^{k_2}} \subseteq \mathbb{Z}_{p^\infty}$ which proves that $\mathbb{Z}_{p^\infty}$ is a subgroup of the unit circle.

All subgroups of $\mathbb{Z}_{p^\infty}$ are finite

Let $H$ be a proper subgroup of $\mathbb{Z}_{p^\infty}$. We prove that $H$ is equal to one of the $\mathbb{Z}_{p^n}$ for $n \ge 0$. If the set of the orders of elements of $H$ is infinite, then for all element $z \in \mathbb{Z}_{p^\infty}$ of order $p^k$, there would exist an element $z^\prime \in H$ of order $p^{k^\prime} > p^k$. Hence $H$ would contain $\mathbb{Z}_{p^\prime}$ and $z \in H$. Finally $\mathbb{Z}_{p^\infty}$ would be included in $H$ in contradiction with the hypothesis that $H$ is a proper subgroup.

Therefore the set of the orders of the elements of $H$ is finite. If $h \in H$ is an element with maximum order $p^n$, we have $H = \mathbb{Z}_{p^n}$.

In conclusion:

• $\mathbb{Z}_{p^\infty}$ is an infinite group whose proper subgroups are all finite.
• It is a non-cyclic group whose all proper subgroups are cyclic.