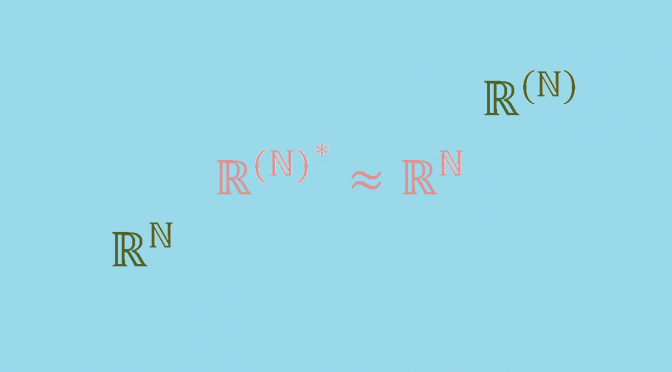In this page \(\mathbb{F}\) refers to a field. Given any vector space \(V\) over \(\mathbb{F}\), the dual space \(V^*\) is defined as the set of all linear functionals \(f: V \mapsto \mathbb{F}\). The dual space \(V^*\) itself becomes a vector space over \(\mathbb{F}\) when equipped with the following addition and scalar multiplication:
\[\left\{
\begin{array}{lll}(\varphi + \psi)(x) & = & \varphi(x) + \psi(x) \\
(a \varphi)(x) & = & a (\varphi(x)) \end{array} \right. \] for all \(\phi, \psi \in V^*\), \(x \in V\), and \(a \in \mathbb{F}\).
There is a natural homomorphism \(\Phi\) from \(V\) into the double dual \(V^{**}\), defined by \((\Phi(v))(\phi) = \phi(v)\) for all \(v \in V\), \(\phi \in V^*\). This map \(\Phi\) is always injective.

Finite-dimensional case

Given a basis \(\{\textbf{e}_1, \dots, \textbf{e}_n\}\) in \(V\), it is possible to construct a specific basis in \(V^*\), called the dual basis. This dual basis is a set \(\{\textbf{e}^*_1,\dots,\textbf{e}^*_n\}\) of linear functionals on \(V\), defined by the relations:
\[\mathbf{e}^*_i(\mathbf{e}_j) = \delta^{i}_{j} \mbox{ for } 1 \leq i \leq n, 1 \leq j \leq n\] where \(\delta^{i}_{j}\) is the Kronecker delta symbol.
Therefore, if \(V\) is finite-dimensional, \(\dim V^{**} = \dim V^* = \dim V\) and \(\Phi\) is an isomorphism.

A counter-example in the infinite-dimensional case

Let \(E=\mathbb{F}^{(\mathbb{N})}\) denote the vector space of sequences of elements of \(\mathbb{F}\) that are eventually \(0\) and \((e_i)_{n \in \mathbb{N}}\) its canonical basis. Also let \(V=\mathbb{F}^{\mathbb{N}}\) denote the vector space of sequences of elements of \(\mathbb{F}\). For \(v=(v_n) \in V\), let define \(\varphi_v \in E^*\) by:
\[\varphi_v(a)= \sum_{n=0}^\infty a_n v_n\] for \(a=(a_n) \in E\) (the sum exists as \(a=(a_n)\) is eventually \(0\)).
The map:
\[\Theta : \left|
\begin{array}{ll} V & \longrightarrow E^*\\
v & \longmapsto \varphi_v \end{array} \right. \] is an injective linear map. On the other hand, let’s take \(\varphi \in E^*\) and note \(u_n=\varphi(e_n)\) for \(n \in \mathbb{N}\). We have \(\varphi = \varphi_u\) with \(u=(u_n)\). Which proves that \(\Theta\) is an isomorphism.
Assuming axiom of choice, and taking the field of real numbers as \(\mathbb{F}\), \(V\) has a basis and has uncountable dimension, whereas \(E\) has countable dimension.
So \(\dim E < \dim E^* = \dim V \leq \dim E^{**}\) and \(E\) cannot be isomorphic to its double-dual. In fact, assuming axiom of choice an infinite-dimension vector space is never isomorph to its double dual.