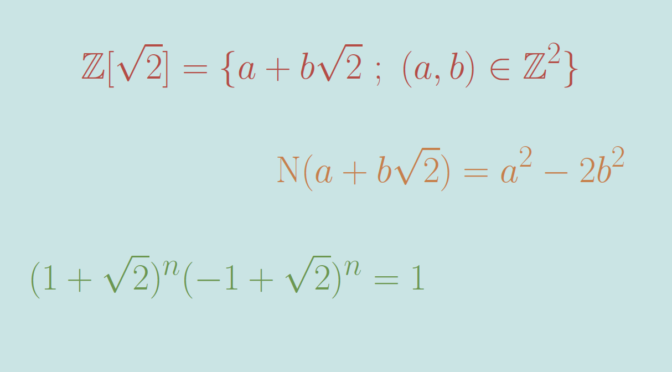In a ring \(R\) a unit is any element \(u\) that has a multiplicative inverse \(v\), i.e. an element \(v\) such that \[
uv=vu=1,\] where \(1\) is the multiplicative identity.

The only units of the commutative ring \(\mathbb Z\) are \(-1\) and \(1\). For a field \(\mathbb F\) the units of the ring \(\mathrm M_n(\mathbb F)\) of the square matrices of dimension \(n \times n\) is the general linear group \(\mathrm{GL}_n(\mathbb F)\) of the invertible matrices. The group \(\mathrm{GL}_n(\mathbb F)\) is infinite if \(\mathbb F\) is infinite, but the ring \(\mathrm M_n(\mathbb F)\) is not commutative for \(n \ge 2\).

The commutative ring \(\mathbb Z[\sqrt{2}] = \{a + b\sqrt{2} \ ; \ (a,b) \in \mathbb Z^2\}\) is not a field. However it has infinitely many units.

\(a + b\sqrt{2}\) is a unit if and only if \(a^2-2b^2 = \pm 1\)

For \(u = a + b\sqrt{2} \in \mathbb Z[\sqrt{2}]\) we denote \(\mathrm N(u) = a^2- 2b^2 \in \mathbb Z\). For any \(u,v \in \mathbb Z[\sqrt{2}]\) we have \(\mathrm N(uv) = \mathrm N(u) \mathrm N(v)\). Therefore for a unit \(u \in \mathbb Z[\sqrt{2}]\) with \(v\) as multiplicative inverse, we have \(\mathrm N(u) \mathrm N(v) = 1\) and \(\mathrm N(u) =a^2-2b^2 \in \{-1,1\}\).

The elements \((1+\sqrt{2})^n\) for \(n \in \mathbb N\) are unit elements

The proof is simple as for \(n \in \mathbb N\) \[
(1+\sqrt{2})^n (-1 + \sqrt{2})^n = \left((1+\sqrt{2})(-1 + \sqrt{2})\right)^n=1\]

One can prove (by induction on \(b\)) that the elements \((1+\sqrt{2})^n\) are the only units \(u \in \mathbb Z[\sqrt{2}]\) for \(u \gt 1\).