Let’s recall that an ordered field \(K\) is said to be Archimedean if for any \(a,b \in K\) such that \(0 \lt a \lt b\) it exists a natural number \(n\) such that \(na > b\).
The ordered fields \(\mathbb Q\) or \(\mathbb R\) are Archimedean. We introduce here the example of an ordered field which is not Archimedean. Let’s consider the field of rational functions
\[\mathbb R(x) = \left\{\frac{S(x)}{T(x)} \ | \ S, T \in \mathbb R[x] \right\}\] For \(f(x)=\frac{S(x)}{T(x)} \in \mathbb R(x)\) we can suppose that the polynomials have a constant polynomial greatest common divisor.
Now we define \(P\) as the set of elements \(f(x)=\frac{S(x)}{T(x)} \in \mathbb R(x)\) in which the leading coefficients of \(S\) and \(T\) have the same sign.
One can verify that the subset \(P \subset \mathbb R(x)\) satisfies following two conditions:
- ORD 1
- Given \(f(x) \in \mathbb R(x)\), we have either \(f(x) \in P\), or \(f(x)=0\), or \(-f(x) \in P\), and these three possibilities are mutually exclusive. In other words, \(\mathbb R(x)\) is the disjoint union of \(P\), \(\{0\}\) and \(-P\).
- ORD 2
- For \(f(x),g(x) \in P\), \(f(x)+g(x)\) and \(f(x)g(x)\) belong to \(P\).
This means that \(P\) is a positive cone of \(\mathbb R(x)\). Hence, \(\mathbb R(x)\) is ordered by the relation
\[f(x) > 0 \Leftrightarrow f(x) \in P.\]
Now let’s consider the rational fraction \(h(x)=\frac{x}{1} \in \mathbb R(x)\). \(h(x)\) is a positive element, i.e. belongs to \(P\) as \(h-1 = \frac{x-1}{1}\). For any \(n \in \mathbb N\), we have
\[h – n 1=\frac{x-n}{1} \in P\] as the leading coefficients of \(x-n\) and \(1\) are both equal to \(1\). Therefore, we have \(h \gt n 1\) for all \(n \in \mathbb N\), proving that \(\mathbb R(x)\) is not Archimedean.

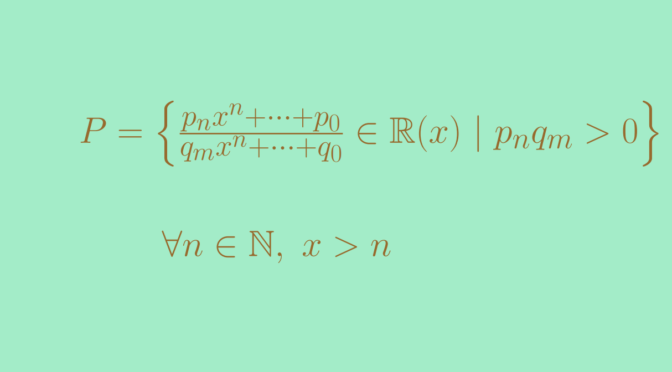
One thought on “A non Archimedean ordered field”