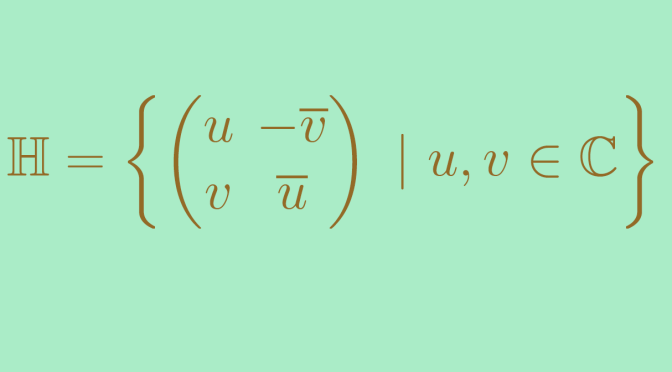We give here an example of a division ring which is not commutative. According to Wedderburn theorem every finite division ring is commutative. So we must turn to infinite division rings to find a non-commutative one, i.e. a skew field.

Let’s introduce the skew field of the Hamilton’s quaternions $$\mathbb H = \left\{\begin{pmatrix} u & -\overline{v} \\ v & \overline{u} \end{pmatrix} \ | \ u,v \in \mathbb C\right\}$$

$\mathbb H$ is a subring of $\mathcal M_2(\mathbb C)$ (the set of matrices of dimension $2$ over $\mathbb C$)

One can easily verify that the identity matrix is an element of $\mathbb H$ taking $(u,v)=(1,0)$. Also the sum and the product of two elements of $\mathbb H$ belong to $\mathbb H$.

The non-zero elements of $\mathbb H$ are invertible

Take $(0,0) \neq (u,v) \in \mathbb C^2$. The determinant of $A=\begin{pmatrix} u & -\overline{v} \\ v & \overline{u} \end{pmatrix}$ is $\delta=\det A = \vert u \vert^2 + \vert v \vert^2 >0$. Hence $A$ is invertible and $$A^{-1}=\frac{1}{\delta}\begin{pmatrix} \overline{u} & \overline{v} \\ -v & u \end{pmatrix}$$

Hence $\mathbb H$ is a division ring.

$\mathbb H$ is not commutative

We denote $\textbf{id}=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$,
$i=\begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}$, $j=\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$ and $k=\begin{pmatrix} 0 & i \\ i & 0 \end{pmatrix}$. All are elements of $\mathbb H$. The identities hold $$i^2=j^2=k^2=ijk=-1$$ as well as following ones
$$ij=-ji=k$$ $$jk=-kj=i$$ $$ki=-ik=j$$
proving that $\mathbb H$ is not commutative. $\mathbb H$ is a skew field.

$\mathbb H$ is a vector space of dimension $4$ over $\mathbb R$

One can verify that any matrix $P=\begin{pmatrix} a+bi & c+di \\ -c+di & a-bi \end{pmatrix}$ of $\mathbb H$ (with $a,b,c,d \in \mathbb R^4$) can be written $$P=a \textbf{id} + bi +cj +dk$$ As $(\textbf{id}, i, j, k)$ is an independent family, it is a basis of $\mathbb H$. Hence the result. One can also verify that $\mathbb R \textbf{id}$ is included in $\mathbb H$ center.