We raise here the following question: “can a vector space \(E\) be written as a finite union of proper subspaces”?

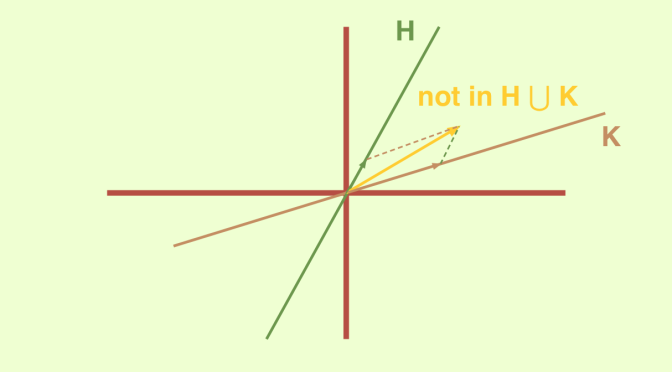
Let’s consider the simplest case, i.e. writing \(E= V_1 \cup V_2\) as a union of two proper subspaces. By hypothesis, one can find two non-zero vectors \(v_1,v_2\) belonging respectively to \(V_1 \setminus V_2\) and \(V_2 \setminus V_1\). The relation \(v_1+v_2 \in V_1\) leads to the contradiction \(v_2 = (v_1+v_2)-v_1 \in V_1\) while supposing \(v_1+v_2 \in V_2\) leads to the contradiction \(v_1 = (v_1+v_2)-v_2 \in V_2\). Therefore, a vector space can never be written as a union of two proper subspaces.

We now analyze if a vector space can be written as a union of \(n \ge 3\) proper subspaces. We’ll see that it is impossible when \(E\) is a vector space over an infinite field. But we’ll describe a counterexample of a vector space over the finite field \(\mathbb{Z}_2\) written as a union of three proper subspaces.

The case of a vector space over an infinite field

We consider a vector space \(E\) over an infinite field, for instance \(\mathbb{R}\) or \(\mathbb{C}\). Suppose that \(\displaystyle E= \bigcup_{k=1}^n V_k\) is the union of \(n \ge 2\) proper subspaces and that \(n\) is minimal, i.e. that \(E\) cannot be written as a union of less than \(n\) subspaces where the subspaces are chosen in \(\{V_1, \dots,V_n\}\). Thus in each \(V_k\), there is a vector \(v_k\) not in the union of the other \(V_{k^\prime}\). In \(S=\{t v_1 + (1-t) v_2; 0 < t < 1 \}\) there are infinitely many vectors and so two different ones among them must belong to some subspace, say \(V_{k^\prime}\). But then \(S \subset V_{k^\prime}\), hence the contradiction \(v_1,v_2 \in V_{k^\prime}\).

The case of a vector space over the finite field \(\mathbb{Z}_2\)

We now take for \(E\) the “plane” \(\mathbb{Z}_2^2\) and consider the three “lines” \(V_1=\mathbb{Z}_2 \cdot e_1\), \(V_2=\mathbb{Z}_2 \cdot e_2\) and \(V_3=\mathbb{Z}_2 \cdot (e_1+e_2)\) where \((e_1,e_2)\) is the canonical basis.
\(E\) is equal to the set of four vectors \(\{(0,0),(1,0),(0,1),(1,1)\}\) and it is easy to verify that \(E=V_1 \cup V_2 \cup V_3\).