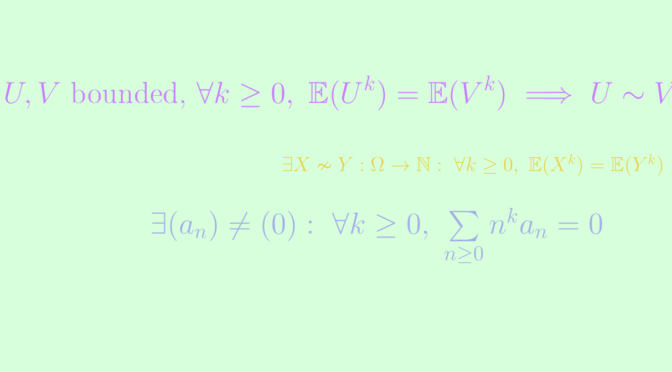The question of the determinacy (or uniqueness) in the moment problem consists in finding whether the moments of a real-valued random variable determine uniquely its distribution. If we assume the random variable to be a.s. bounded, uniqueness is a consequence of Weierstrass approximation theorem.

Given the moments, the distribution need not be unique for unbounded random variables. Carleman’s condition states that for two positive random variables \(X, Y\) with the same finite moments for all orders, if \(\sum\limits_{n \ge 1} \frac{1}{\sqrt[2n]{\mathbb{E}(X^n)}} = +\infty\), then \(X\) and \(Y\) have the same distribution. In this article we describe random variables with different laws but sharing the same moments, on \(\mathbb R_+\) and \(\mathbb N\).

Continuous case on \(\mathbb{R}_+\)

In the article a non-zero function orthogonal to all polynomials, we described a function \(f\) orthogonal to all polynomials in the sense that \[
\forall k \ge 0,\ \displaystyle{\int_0^{+\infty}} x^k f(x)dx = 0 \tag{O}.\]

This function was \(f(u) = \sin\big(u^{\frac{1}{4}}\big)e^{-u^{\frac{1}{4}}}\). This inspires us to define \(U\) and \(V\) with values in \(\mathbb R^+\) by: \[\begin{cases}
f_U(u) &= \frac{1}{24}e^{-\sqrt[4]{u}}\\
f_V(u) &= \frac{1}{24}e^{-\sqrt[4]{u}} \big( 1 + \sin(\sqrt[4]{u})\big)
\end{cases}\]

Both functions are positive. Since \(f\) is orthogonal to the constant map equal to one and \(\displaystyle{\int_0^{+\infty}} f_U = \displaystyle{\int_0^{+\infty}} f_V = 1\), they are indeed densities. One can verify that \(U\) and \(V\) have moments of all orders and \(\mathbb{E}(U^k) = \mathbb{E}(V^k)\) for all \(k \in \mathbb N\) according to orthogonality relation \((\mathrm O)\) above.

Discrete case on \(\mathbb N\)

In this section we define two random variables \(X\) and \(Y\) with values in \(\mathbb N\) having the same moments. Let’s take an integer \(q \ge 2\) and set for all \(n \in \mathbb{N}\): \[
\begin{cases}
\mathbb{P}(X=q^n) &=e^{-q}q^n \cdot \frac{1}{n!} \\
\mathbb{P}(Y=q^n) &= e^{-q}q^n\left(\frac{1}{n!} + \frac{(-1)^n}{(q-1)(q^2-1)\cdot\cdot\cdot (q^n-1)}\right)
\end{cases}\]

Both quantities are positive and for any \(k \ge 0\), \(\mathbb{P}(X=q^n)\) and \(\mathbb{P}(Y=q^n) = O_{n \to \infty}\left(\frac{1}{q^{kn}}\right)\). We are going to prove that for all \(k \ge 1\), \( u_k = \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn}}{(q-1)(q^2-1)\cdot\cdot\cdot (q^n-1)}\) is equal to \(0\).

We only need to write following equalities for all \(k \ge 0\): \[\begin{align} u_{k+1} &= \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn} q^n}{\prod \limits_{i=1}^n (q^i-1)} \\&= \sum \limits_{n=1}^{+\infty} \frac{(-1)^n q^{kn} (q^n – 1)}{\prod \limits_{i=1}^n (q^i-1)} + \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn} \cdot 1}{\prod \limits_{i=1}^n (q^i-1)} \\& = – q^k \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn}}{\prod \limits_{i=1}^n (q^i-1)} + \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn} \cdot 1}{\prod \limits_{i=1}^n (q^i-1)} = (1-q^k)u_k \end{align}\]

As \(u_1=0\) we get by induction, \(u_k = 0\) for all \(k \ge 1\). With this, we can conclude both measures sum to \(1\) for \(k=1\), and that \(X\) and \(Y\) have the same moments.

Byproduct: existence of a non zero integer series with all derivatives equal to zero

For a discrete random variable \(X\) with values in \(\mathbb{N}\) and having finite moments of all orders, the generating function \(\mathcal{G}_X(s) = \mathbb{E}\left(s^X\right)\) is a smooth function on \([0,1]\) and \(\mathcal{G}_X^{(k)}(1) = \mathbb{E}(X^k)\) for all \(k \ge 0\).

Denote \(a_n := \mathbb{P}(X=n) – \mathbb{P}(Y=n)\). As mentioned above, the integer series \(S(x) = \sum \limits_{n=0}^{+\infty} a_n x^n\) and all its derivatives converge on \([0,1]\). Also, \(a_1 = -e^{-q}\) so \(f\) is non zero. Yet, for all \(k \ge 0\), \[ f^{(k)}(1) = \mathbb{E}(X^k) – \mathbb{E}(Y^k) = 0.\]

Note: This cannot happen if \(1\) is in the disk of convergence. In that case, \(\sqrt[q^n]{|a_{q^n}|} \sim_{n \to \infty} 1\) , so \(1\) is indeed on the boundary of the disk of convergence of \(S\).