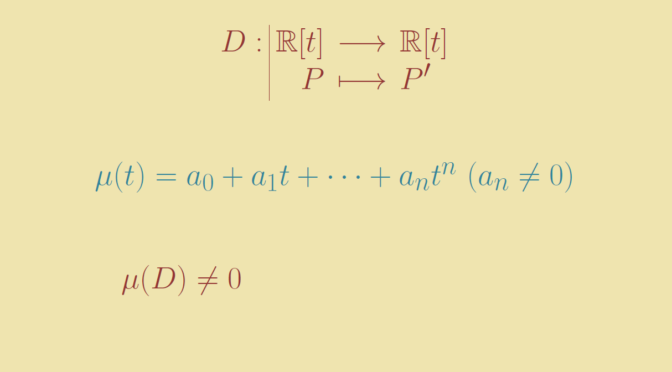Given an endomorphism \(T\) on a finite-dimensional vector space \(V\) over a field \(\mathbb F\), the minimal polynomial \(\mu_T\) of \(T\) is well defined as the generator (unique up to units in \(\mathbb F\)) of the ideal:\[
I_T= \{p \in \mathbb F[t]\ ; \ p(T)=0\}.\]

For infinite-dimensional vector spaces, the minimal polynomial might not be defined. Let’s provide an example.

We take the real polynomials \(V = \mathbb R [t]\) as a real vector space and consider the derivative map \(D : P \mapsto P^\prime\). Let’s prove that \(D\) doesn’t have any minimal polynomial. By contradiction, suppose that \[
\mu_D(t) = a_0 + a_1 t + \dots + a_n t^n \text{ with } a_n \neq 0\] is the minimal polynomial of \(D\), which means that for all \(P \in \mathbb R[t]\) we have \[
a_0 + a_1 P^\prime + \dots + a_n P^{(n)} = 0.\] Taking for \(P\) the polynomial \(t^n\) we get \[
a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n = 0,\] which doesn’t make sense as \(n! a_n \neq 0\), hence \(a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n\) cannot be the zero polynomial.

We conclude that \(D\) doesn’t have any minimal polynomial.