Let $V$ be a real vector space endowed with an Euclidean norm $\Vert \cdot \Vert$.

A bijective map $T : V \to V$ that preserves inner product $\langle \cdot, \cdot \rangle$ is linear. Also, Mazur-Ulam theorem states that an onto map $T : V \to V$ which is an isometry ($\Vert T(x)-T(y) \Vert = \Vert x-y \Vert$ for all $x,y \in V$) and fixes the origin ($T(0) = 0$) is linear.

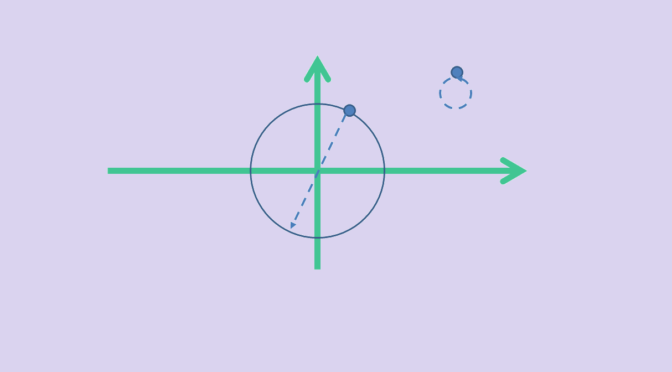
What about an application that preserves the norm ($\Vert T(x) \Vert = \Vert x \Vert$ for all $x \in V$)? $T$ might not be linear as we show with following example: $$\begin{array}{l|rcll} T : & V & \longrightarrow & V \\ & x & \longmapsto & x & \text{if } \Vert x \Vert \neq 1\\ & x & \longmapsto & -x & \text{if } \Vert x \Vert = 1\end{array}$$

It is clear that $T$ preserves the norm. However $T$ is not linear as soon as $V$ is not the zero vector space. In that case, consider $x_0$ such that $\Vert x_0 \Vert = 1$. We have: $$\begin{cases} T(2 x_0) &= 2 x_0 \text{ as } \Vert 2 x_0 \Vert = 2\\ \text{while}\\ T(x_0) + T(x_0) = -x_0 + (-x_0) &= – 2 x_0 \end{cases}$$