Monthly Archives: September 2016

Analysis

Counterexample around L’Hôpital’s rule

Leave a comment

Let us consider two differentiable functions \(f\) and \(g\) defined in an open interval \((a,b)\), where \(b\) might be \(\infty\). If
\[\lim\limits_{x \to b^-} f(x) = \lim\limits_{x \to b^-} g(x) = \infty\] and if \(g^\prime(x) \neq 0\) in some interval \((c,b)\), then a version of l’Hôpital’s rule states that \(\lim\limits_{x \to b^-} \frac{f^\prime(x)}{g^\prime(x)} = L\) implies \(\lim\limits_{x \to b^-} \frac{f(x)}{g(x)} = L\).

We provide a counterexample when \(g^\prime\) vanishes in all neighborhood of \(b\). The counterexample is due to the Austrian mathematician Otto Stolz.

We take \((0,\infty)\) for the interval \((a,b)\) and \[
\begin{cases}
f(x) &= x + \cos x \sin x\\
g(x) &= e^{\sin x}(x + \cos x \sin x)
\end{cases}\] which derivatives are \[
\begin{cases}
f^\prime(x) &= 2 \cos^2 x\\
g^\prime(x) &= e^{\sin x} \cos x (x + \cos x \sin x + 2 \cos x)
\end{cases}\] We have \[
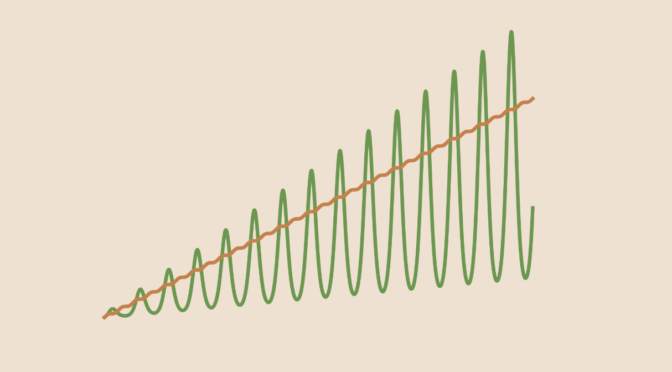
\lim\limits_{x \to \infty} \frac{f^\prime(x)}{g^\prime(x)} = \lim\limits_{x \to \infty} \frac{2 \cos x}{e^{\sin x} (x + \cos x \sin x + 2 \cos x)} = 0,\] however \[
\frac{f(x)}{g(x)} = \frac{1}{e^{\sin x}}\] doesn’t have any limit at \(\infty\) as it oscillates between \(\frac{1}{e}\) and \(e\).

Analysis

The Schwarz lantern

Leave a comment

Consider a smooth curve defined by a continuous map \(f : [0,1] \to \mathbb R^n\) with \(n \ge 2\) where \(f\) is supposed to have a continuous derivative. One can prove that the curve is rectifiable, its arc length being \[
L = \lim\limits_{n \to \infty} \sum_{i=1}^n \vert f(t_i) – f(t_{i-1}) \vert = \int_0^1 \vert f^\prime (t) \vert \ dt\] with \(t_i = \frac{i}{n}\) for \(0 \le i \le n\).

What can happen when we consider a surface instead of a curve?

Consider a compact, smooth surface (possibly with boundary) embedded in \(\mathbb R^3\). We can approximate it as a polyhedral surface composed of small triangles with all vertices on the initial surface. Will the sum of the areas of the triangles converges to the area of the surface if their size is converging to zero?

The answer is negative and we provide a counterexample named Schwarz lantern. We take a cylinder of radius \(r\) and height \(h\). We approximate the cylinder by \(4nm\) isosceles triangles positioned as in the picture in \(2n\) slices. All triangles have the same base and height given by \[
b = 2r \sin \left(\frac{\pi}{m}\right), \ h = \sqrt{r^2 \left[1-\cos \left(\frac{\pi}{m}\right)\right]^2+\left(\frac{h}{2n}\right)^2}\] Hence the area of the polyhedral surface is \[
\begin{aligned}
S^\prime(m,n) &= 4 m n r \sin \left(\frac{\pi}{m}\right) \sqrt{r^2 \left[1-\cos \left(\frac{\pi}{m}\right)\right]^2+\left(\frac{h}{2n}\right)^2}\\
&= 4 m n r \sin \left(\frac{\pi}{m}\right) \sqrt{4 r^2 \sin^4 \left(\frac{\pi}{2m} \right)+\left(\frac{h}{2n}\right)^2}
\end{aligned}\] From there, let’s have a look to the value of \(S^\prime(m,n)\) as \(m,n \to \infty\).

Continue reading The Schwarz lantern →

Analysis

Counterexamples around Lebesgue’s Dominated Convergence Theorem

Leave a comment

Let’s recall Lebesgue’s Dominated Convergence Theorem. Let \((f_n)\) be a sequence of real-valued measurable functions on a measure space \((X, \Sigma, \mu)\). Suppose that the sequence converges pointwise to a function \(f\) and is dominated by some integrable function \(g\) in the sense that \[
\vert f_n(x) \vert \le g (x)\] for all \(n \in \mathbb N\) and all \(x \in X\).
Then \(f\) is integrable and \[
\lim\limits_{n \to \infty} \int_X f_n(x) \ d \mu = \int_X f(x) \ d \mu\]

Let’s see what can happen if we drop the domination condition.

We consider the space \(\mathbb R\) endowed with Lebesgue measure and for \(E \subseteq \mathbb R\) we denote by \(\chi_E\) the indicator function of \(E\) defined by \[
\chi_E(x)=\begin{cases}
1 \text{ if } x \in E\\
0 \text{ otherwise}\end{cases}\] For \(n \in \mathbb N\), the function \(f_n=\frac{1}{2n}\chi_{(n^2-n,n^2+n)}\) is measurable and we have \[
\int_{\mathbb R} \frac{1}{2n}\chi_{(n^2-n,n^2+n)}(x) \ dx = \int_{n^2-n}^{n^2+n} \frac{1}{2n} \ dx = 1\] The sequence \((f_n)\) converges uniformly (and therefore pointwise) to the always vanishing function as for \(n \in \mathbb N\) we have for all \(x \in \mathbb R\) \(\vert f_n(x) \vert \le \frac{1}{2n}\). Hence the conclusion of Lebesgue’s Dominated Convergence Theorem doesn’t hold for the sequence \((f_n)\).

Let’s verify that the sequence \((f_n)\) is not dominated by some integrable function \(g\). For \(p < q\) integers, we have \[ \begin{aligned} q^2-q-(p^2+p) &= q^2-p^2 -q-p\\ &= (q-p)(q+p) -q -p\\ &\ge (q+p) -q-p=0 \end{aligned}\] Hence for \(p \neq q\) integers the intervals \((p^2-p,p^2+p)\) and \((q^2-q,q^2+q)\) are disjoint. Consequently for all \(x \in \mathbb R\) the sum \(\sum_{n \in \mathbb N} f_n(x)\) amounts to only one term and the function \(\sum_{n \in \mathbb N} f_n\) is well defined. If \(g\) dominates the sequence \((f_n)\), it satisfies \(0 \le \sum_{n \in \mathbb N} f_n \le g\). But \[ \int_{\mathbb R} \sum_{n \in \mathbb N} f_n(x) \ dx = \sum_{n \in \mathbb N} \int_{\mathbb R} f_n(x) \ dx = \sum_{n \in \mathbb N} 1 = \infty\] and \(g\) cannot be integrable. Continue reading Counterexamples around Lebesgue’s Dominated Convergence Theorem →