Monthly Archives: July 2016

Algebra

Non linear map preserving orthogonality

Leave a comment

Let \(V\) be a real vector space endowed with an inner product \(\langle \cdot, \cdot \rangle\).

It is known that a bijective map \( T : V \to V\) that preserves the inner product \(\langle \cdot, \cdot \rangle\) is linear.

That might not be the case if \(T\) is supposed to only preserve orthogonality. Let’s consider for \(V\) the real plane \(\mathbb R^2\) and the map \[
\begin{array}{l|rcll}
T : & \mathbb R^2 & \longrightarrow & \mathbb R^2 \\
& (x,y) & \longmapsto & (x,y) & \text{for } xy \neq 0\\
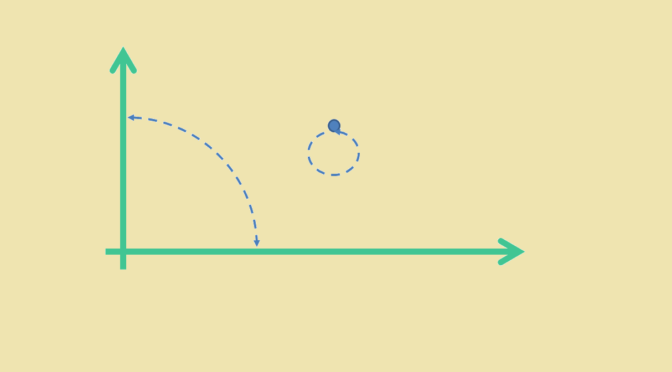
& (x,0) & \longmapsto & (0,x)\\
& (0,y) & \longmapsto & (y,0) \end{array}\]

The restriction of \(T\) to the plane less the x-axis and the y-axis is the identity and therefore is bijective on this set. Moreover \(T\) is a bijection from the x-axis onto the y-axis, and a bijection from the y-axis onto the x-axis. This proves that \(T\) is bijective on the real plane.

\(T\) preserves the orthogonality on the plane less x-axis and y-axis as it is the identity there. As \(T\) swaps the x-axis and the y-axis, it also preserves orthogonality of the coordinate axes. However, \(T\) is not linear as for non zero \(x \neq y\) we have: \[
\begin{cases}
T[(x,0) + (0,y)] = T[(x,y)] &= (x,y)\\
\text{while}\\
T[(x,0)] + T[(0,y)] = (0,x) + (y,0) &= (y,x)
\end{cases}\]

Topology

The line with two origins

2 Comments

Let’s introduce and describe some properties of the line with two origins.

Let \(X\) be the union of the set \(\mathbb R \setminus \{0\}\) and the two-point set \(\{p,q\}\). The line with two origins is the set \(X\) topologized by taking as base the collection \(\mathcal B\) of all open intervals in \(\mathbb R\) that do not contain \(0\), along with all sets of the form \((-a,0) \cup \{p\} \cup (0,a)\) and all sets of the form \((-a,0) \cup \{q\} \cup (0,a)\), for \(a > 0\).

\(\mathcal B\) is a base for a topology \(\mathcal T\) of \(X\)

Indeed, one can verify that the elements of \(\mathcal B\) cover \(X\) as \[
X = \left( \bigcup_{a > 0} (-a,0) \cup \{p\} \cup (0,a) \right) \cup \left( \bigcup_{a > 0} (-a,0) \cup \{q\} \cup (0,a) \right)\] and that the intersection of two elements of \(\mathcal B\) is the union of elements of \(\mathcal B\) (verification left to the reader).

Each of the spaces \(X \setminus \{p\}\) and \(X \setminus \{q\}\) is homeomorphic to \(\mathbb R\)

Let’s prove it for \(X \setminus \{p\}\). The map \[
\begin{array}{l|rcll}
f : & X \setminus \{p\} & \longrightarrow & \mathbb R \\
& x & \longmapsto & x & \text{for } x \neq q\\
& q & \longmapsto & 0 \end{array}\] is a bijection. \(f\) is continuous as the inverse image of an open interval \(I\) of \(\mathbb R\) is an open subset of \(X\). For example taking \(I=(-b,c)\) with \(0 < b < c\), we have \begin{align*} f^{-1}[I] &= (-b,0) \cup \{q\} \cup (0,c)\\ &= \left( (-b,0) \cup \{q\} \cup (0,b) \right) \cup (b/2,c) \end{align*} One can also prove that \(f^{-1}\) is continuous. Continue reading The line with two origins →

Analysis

A power series converging everywhere on its circle of convergence defining a non-continuous function

Leave a comment

Consider a complex power series \(\displaystyle \sum_{k=0}^\infty a_k z^k\) with radius of convergence \(0 \lt R \lt \infty\) and suppose that for every \(w\) with \(\vert w \vert = R\), \(\displaystyle \sum_{k=0}^\infty a_k w^k\) converges.

We provide an example where the power expansion at the origin \[
\displaystyle f(z) = \sum_{k=0}^\infty a_k z^k\] is discontinuous on the closed disk \(\vert z \vert \le R \).

The function \(f\) is constructed as an infinite sum \[
\displaystyle f(z) = \sum_{n=1}^\infty f_n(z)\] with \(f_n(z) = \frac{\delta_n}{a_n-z}\) where \((\delta_n)_{n \in \mathbb N}\) is a sequence of positive real numbers and \((a_n)\) a sequence of complex numbers of modulus larger than one and converging to one. Let \(f_n^{(r)}(z)\) denote the sum of the first \(r\) terms in the power series expansion of \(f_n(z)\) and \(\displaystyle f^{(r)}(z) \equiv \sum_{n=1}^\infty f_n^{(r)}(z)\).

We’ll prove that:

  1. If \(\sum_n \delta_n \lt \infty\) then \(\sum_{n=1}^\infty f_n^{(r)}(z)\) converges and \(f(z) = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(z)\) for \(\vert z \vert \le 1\) and \(z \neq 1\).
  2. If \(a_n=1+i \epsilon_n\) and \(\sum_n \delta_n/\epsilon_n < \infty\) then \(\sum_{n=1}^\infty f_n^{(r)}(1)\) converges and \(f(1) = \lim\limits_{r \to \infty} \sum_{n=1}^\infty f_n^{(r)}(1)\)
  3. If \(\delta_n/\epsilon_n^2 \to \infty\) then \(f(z)\) is unbounded on the disk \(\vert z \vert \le 1\).

First, let’s recall this corollary of Lebesgue’s dominated convergence theorem:

Let \((u_{n,i})_{(n,i) \in \mathbb N \times \mathbb N}\) be a double sequence of complex numbers. Suppose that \(u_{n,i} \to v_i\) for all \(i\) as \(n \to \infty\), and that \(\vert u_{n,i} \vert \le w_i\) for all \(n\) with \(\sum_i w_i < \infty\). Then for all \(n\) the series \(\sum_i u_{n,i}\) is absolutely convergent and \(\lim_n \sum_i u_{n,i} = \sum_i v_i\).
Continue reading A power series converging everywhere on its circle of convergence defining a non-continuous function →

Algebra

A linear map having all numbers as eigenvalue

Leave a comment

Consider a linear map \(\varphi : E \to E\) where \(E\) is a linear space over the field \(\mathbb C\) of the complex numbers. When \(E\) is a finite dimensional vector space of dimension \(n \ge 1\), the number of eigenvalues is finite. The eigenvalues are the roots of the characteristic polynomial \(\chi_\varphi\) of \(\varphi\). \(\chi_\varphi\) is a complex polynomial of degree \(n \ge 1\). Therefore the set of eigenvalues of \(\varphi\) is non-empty and its cardinal is less than \(n\).

Things are different when \(E\) is an infinite dimensional space.

A linear map having all numbers as eigenvalue

Let’s consider the linear space \(E=\mathcal C^\infty([0,1])\) of smooth complex functions having derivatives of all orders and defined on the segment \([0,1]\). \(E\) is an infinite dimensional space: it contains all the polynomial maps.

On \(E\), we define the linear map \[\begin{array}{l|rcl}
\varphi : & \mathcal C^\infty([0,1]) & \longrightarrow & \mathcal C^\infty([0,1]) \\
& f & \longmapsto & f^\prime \end{array}\]

The set of eigenvalues of \(\varphi\) is all \(\mathbb C\). Indeed, for \(\lambda \in \mathbb C\) the map \(t \mapsto e^{\lambda t}\) is an eigenvector associated to the eigenvalue \(\lambda\).

A linear map having no eigenvalue

On the same linear space \(E=\mathcal C^\infty([0,1])\), we now consider the linear map \[\begin{array}{l|rcl}
\psi : & \mathcal C^\infty([0,1]) & \longrightarrow & \mathcal C^\infty([0,1]) \\
& f & \longmapsto & x f \end{array}\]

Suppose that \(\lambda \in \mathbb C\) is an eigenvalue of \(\psi\) and \(h \in E\) an eigenvector associated to \(\lambda\). By hypothesis, there exists \(x_0 \in [0,1]\) such that \(h(x_0) \neq 0\). Even better, as \(h\) is continuous, \(h\) is non-vanishing on \(J \cap [0,1]\) where \(J\) is an open interval containing \(x_0\). On \(J \cap [0,1]\) we have the equality \[
(\psi(h))(x) = x h(x) = \lambda h(x)\] Hence \(x=\lambda\) for all \(x \in J \cap [0,1]\). A contradiction proving that \(\psi\) has no eigenvalue.