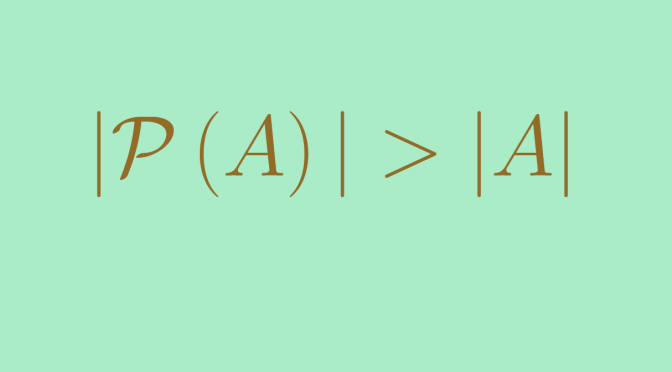We have seen in this article several sets that are infinite and countable. Namely, the set of natural numbers \(\mathbb N\), the set of integers \(\mathbb Z\), the set of rational numbers \(\mathbb Q\). We have seen that the product \(\mathbb N \times \mathbb N\) is also countable. The question then arises, “Are all infinite sets countable?”.

The answer is negative and we prove that \(\mathbb R\) is not countable.

The set of all reals \(\mathbb R\) is not countable

Suppose for the sake of contradiction that \(\mathbb R\) is countable and that \(\mathbb R = \{x_n \ | \ n \in \mathbb N\}\), the \(x_n\) being all distinct. We build by induction two sequences \((a_n)_{n \in \mathbb N}\) increasing and \((b_n)_{n \in \mathbb N}\) decreasing such that:

• \(a_n < b_n\) for all \(n \in \mathbb N\),
• \(\vert a_n – b_n \vert \) converges to zero,
• and \(x_n \notin [a_{n+1},b_{n+1}]\).

Continue reading There is no greatest cardinal →

I follow on here from the initial article on cardinality. In that article, we have seen that \(\mathbb N\) contains an infinite countable subset whose complement is also infinite. Namely the subsets of even and odd integers.

Let’s now consider the set \(\mathbb N \times \mathbb N\). \(\mathbb N \times \mathbb N\) contains a countable infinite number of copies of \(\mathbb N\), as for all \(i \in \mathbb N\), \(\{i\} \times \mathbb N \subset \mathbb N \times \mathbb N\). Surprisingly, it is however possible to define a bijection between \(\mathbb N \times \mathbb N\) and \(\mathbb N\).

\(\mathbb N \times \mathbb N\) is equinumerous to \(\mathbb N\)

Consider the map \[\begin{array}{l|rcl}
\varphi : & \mathbb N \times \mathbb N & \longrightarrow & \mathbb N\\
& (n,m) & \longmapsto & 2^{n-1} (2m-1) \end{array}\] \(\varphi\) is one-to-one. Suppose that \(2^{n_1-1} (2m_1-1) = 2^{n_2-1} (2m_2-1)\). If \(n_1=1\), we must also have \(n_2=1\) as \(2 m_1 – 1\) is odd. That implies \((n_1,m_1)=(n_2,m_2)\). Let’s now suppose \(n_1 >1\). According to Euclid’s lemma, \(2^{n_1-1}\) divides \(2^{n_2-1}\) as \(2^{n_1-1}\) is even and \(2m_2 – 1\) odd. By symmetry \(2^{n_2-1}\) also divides \(2^{n_1-1}\). Finally, \(2^{n_1 – 1} = 2^{n_2 – 1}\), \(n_1 = n_2\) and consequently \(m_1 = m_2\). Continue reading Counterexamples around cardinality (part 2) →

In mathematics, the cardinality of a set is a measure of the “number of elements of the set”. We denote by \(|A|\) the cardinality of the set \(A\). We say that \(A\) and \(B\) have the same cardinality if there exists a bijection from \(A\) onto \(B\). Such sets said to be equinumerous.

The finite sets satisfy the property that if \(A \subset B\) and \(A\) and \(B\) have the same cardinality then \(A=B\). For example take \(A=\{2,5,42\}\). If \(A \subset B\) and \(B\) has more elements than \(A\), a bijection \(f\) from \(A\) to \(B\) cannot exist as an element in \(B \setminus \{f(2),f(5),f(42)\}\) won’t have an inverse image under \(f\).

This becomes false for infinite sets. Let’s give some examples.

Proper subsets of \(\mathbb N\) equinumerous to \(\mathbb N\)

The set \(A\) of the positive even integers is strictly included in \(\mathbb N\): there exist odd positive integers! However, \(A\) is equinumerous to \(\mathbb N\). The map \(f : n \to 2n\) is a bijection from \(A\) onto \(\mathbb N\).

For our second example, consider the set \(\mathbb P\) of prime numbers. We recall that \(\mathbb P\) is infinite. The proof is quite simple by contradiction. Suppose that there is only a finite number \(\{p_1, \dots, p_n\}\) of prime numbers and consider the number \(N = p_1 p_2 \cdots p_n + 1\). As a consequence of the fundamental theorem of arithmetic, a prime \(q\) divides \(N\). However \(q \notin \{p_1, \dots, p_n\}\) as this would imply \(q\) divides \(1\). From there, we can define by induction a bijection from \(\mathbb N\) onto \(\mathbb P\) by defining \[f(n)=\begin{cases}
2 & \text{for } n=1\\
\min (\mathbb P \setminus \{p_1, \dots, p_n\}) & \text{else }
\end{cases}\] Continue reading Counterexamples around cardinality (part 1) →