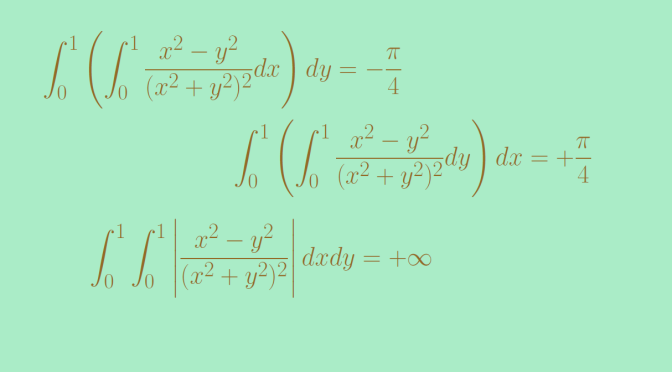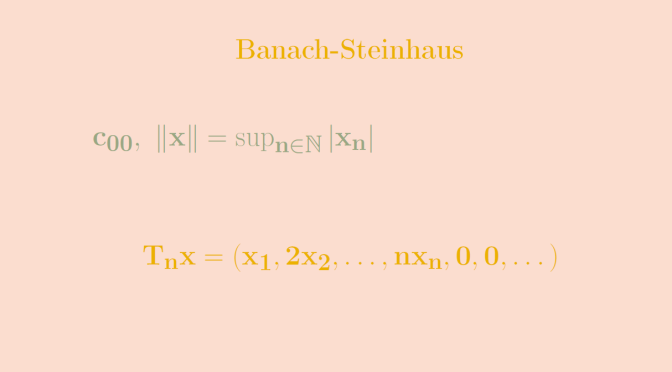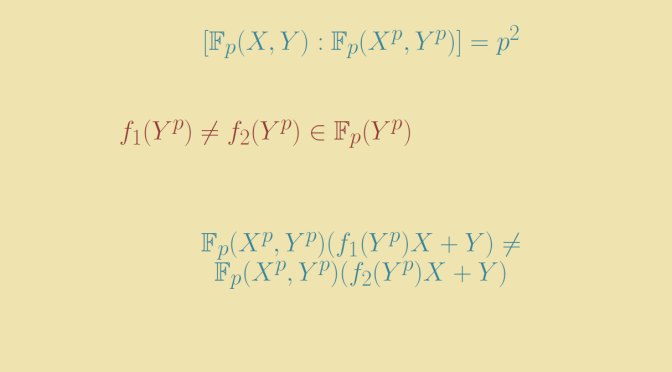Monthly Archives: October 2015

Analysis

Counterexamples around Fubini’s theorem

Leave a comment

We present here some counterexamples around the Fubini theorem.

We recall Fubini’s theorem for integrable functions:
let \(X\) and \(Y\) be \(\sigma\)-finite measure spaces and suppose that \(X \times Y\) is given the product measure. Let \(f\) be a measurable function for the product measure. Then if \(f\) is \(X \times Y\) integrable, which means that \(\displaystyle \int_{X \times Y} \vert f(x,y) \vert d(x,y) < \infty\), we have \[\int_X \left( \int_Y f(x,y) dy \right) dx = \int_Y \left( \int_X f(x,y) dx \right) dy = \int_{X \times Y} f(x,y) d(x,y)\] Let's see what happens when some hypothesis of Fubini's theorem are not fulfilled. Continue reading Counterexamples around Fubini’s theorem →

Topology

Counterexamples around Banach-Steinhaus theorem

Leave a comment

In this article we look at what happens to Banach-Steinhaus theorem when the completness hypothesis is not fulfilled. One form of Banach-Steinhaus theorem is the following one.

Banach-Steinhaus Theorem Let \(T_n : E \to F\) be a sequence of continuous linear maps from a Banach space \(E\) to a normed space \(F\). If for all \(x \in E\) the sequence \(T_n x\) is convergent to \(Tx\), then \(T\) is a continuous linear map.

A sequence of continuous linear maps converging to an unbounded linear map

Let \(c_{00}\) be the vector space of real sequences \(x=(x_n)\) eventually vanishing, equipped with the norm \[\Vert x \Vert = \sup_{n \in \mathbb N} \vert x_n \vert\] For \(n \in \mathbb N\), \(T_n : E \to E\) denotes the linear map defined by \[T_n x = (x_1,2 x_2, \dots, n x_n,0,0, \dots).\] \(T_n\) is continuous as for \(\Vert x \Vert \le 1\), we have
\begin{align*}
\Vert T_n x \Vert &= \Vert (x_1,2 x_2, \dots, n x_n,0,0, \dots) \Vert\\
& = \sup_{1 \le k \le n} \vert k x_k \vert \le n \Vert x \Vert \le n
\end{align*} Continue reading Counterexamples around Banach-Steinhaus theorem →

Algebra

A finite extension that contains infinitely many subfields

Leave a comment

Let’s consider \(K/k\) a finite field extension of degree \(n\). The following theorem holds.

Theorem: the following conditions are equivalent:

  1. The extension contains a primitive element.
  2. The number of intermediate fields between \(k\) and \(K\) is finite.

Our aim here is to describe a finite field extension having infinitely many subfields. Considering the theorem above, we have to look at an extension without a primitive element.

The extension \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) is finite

For \(p\) prime, \(\mathbb F_p\) denotes the finite field with \(p\) elements. \(\mathbb F_p(X,Y)\) is the algebraic fraction field of two variables over the field \(\mathbb F_p\). \(\mathbb F_p(X^p,Y^p)\) is the subfield of \(\mathbb F_p(X,Y)\) generated by the elements \(X^p,Y^p\). Continue reading A finite extension that contains infinitely many subfields →

Topology

Counterexamples around connected spaces

Leave a comment

A connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. We look here at unions and intersections of connected spaces.

Union of connected spaces

The union of two connected spaces \(A\) and \(B\) might not be connected “as shown” by two disconnected open disks on the plane.

union-connected-spaces-image
The union of two connected spaces might not be connected.

However if the intersection \(A \cap B\) is not empty then \(A \cup B\) is connected.

Intersection of connected spaces

The intersection of two connected spaces \(A\) and \(B\) might also not be connected. An example is provided in the plane \(\mathbb R^2\) by taking for \(A\) the circle centered at the origin with radius equal to \(1\) and for \(B\) the segment \(\{(x,0) \ : \ x \in [-1,1]\}\). The intersection \(A \cap B = \{(-1,0),(1,0)\}\) is the union of two points which is not connected.

Analysis

Differentiability of multivariable real functions (part2)

Leave a comment

Following the article on differentiability of multivariable real functions (part 1), we look here at second derivatives. We consider a function \(f : \mathbb R^n \to \mathbb R\) with \(n \ge 2\).

Schwarz’s theorem states that if \(f : \mathbb R^n \to \mathbb R\) has continuous second partial derivatives at any given point in \(\mathbb R^n\), then for \((a_1, \dots, a_n) \in \mathbb R^n\) and \(i,j \in \{1, \dots, n\}\):
\[\frac{\partial^2 f}{\partial x_i \partial x_j}(a_1, \dots, a_n)=\frac{\partial^2 f}{\partial x_j \partial x_i}(a_1, \dots, a_n)\]

A function for which \(\frac{\partial^2 f}{\partial x \partial y}(0,0) \neq \frac{\partial^2 f}{\partial y \partial x}(0,0)\)

We consider:
\[\begin{array}{l|rcl}
f : & \mathbb R^2 & \longrightarrow & \mathbb R \\
& (0,0) & \longmapsto & 0\\
& (x,y) & \longmapsto & \frac{xy(x^2-y^2)}{x^2+y^2} \text{ for } (x,y) \neq (0,0)
\end{array}\] Continue reading Differentiability of multivariable real functions (part2) →