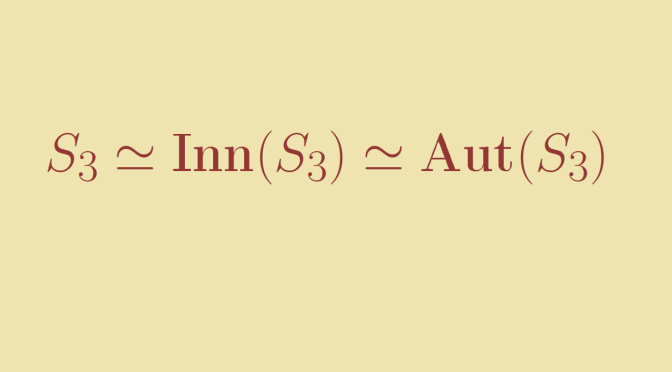A group isomorphic to its automorphism group

September 27, 2015 Jean-Pierre Merx Leave a comment

We consider a group $G$ and we look at its automorphism group $\text{Aut}(G)$ . Can $G$ be isomorphic to
$\text{Aut}(G)$ ? The answer is positive and we’ll prove that it is the case for the symmetric group $S_3$ .

Consider the morphism $\begin{array}{l|rcl} \Phi : & S_3 & \longrightarrow & \text{Aut}(S_3) \\ & a & \longmapsto & \varphi_a \end{array}$
where $\varphi_a$ is the inner automorphism $\varphi_a : x \mapsto a^{-1}xa$ . It is easy to verify that $\Phi$ is indeed a group morphism. The kernel of $\Phi$ is the center of $S_3$ which is having the identity for only element. Hence $\Phi$ is one-to-one and $S_3 \simeq \Phi(S_3)$ . Therefore it is sufficient to prove that $\Phi$ is onto. As $|S_3|=6$ , we’ll be finished if we prove that $|\text{Aut}(S_3)|=6$ .

Generally, for $G_1,G_2$ groups and $f : G_1 \to G_2$ a one-to-one group morphism, the image of an element $x$ of order $k$ is an element $f(x)$ having the same order $k$ . So for $\varphi \in \text{Aut}(S_3)$ the image of a transposition is a transposition. As the transpositions $\{(1 \ 2), (1 \ 3), (2 \ 3)\}$ generate $(S_3)$ , $\varphi$ is completely defined by $\{\varphi((1 \ 2)), \varphi((1 \ 3)), \varphi((2 \ 3))\}$ . We have 3 choices to define the image of $(1 \ 2)$ under $\varphi$ and then 2 choices for the image of $(1 \ 3)$ under $\varphi$ . The image of $(2 \ 3)$ under $\varphi$ is the remaining transposition.

Finally, we have proven that $|\text{Aut}(S_3)|=6$ as desired and $S_3 \simeq \text{Aut}(S_3)$ .

Topology

Playing with interior and closure

September 20, 2015 Jean-Pierre Merx Leave a comment

Let’s play with the closure and the interior of sets.

To start the play, we consider a topological space $E$ and denote for any subspace $A \subset E$ : $\overline{A}$ the closure of $A$ and $\overset{\circ}{A}$ the interior of $A$ .

Warm up with the closure operator

For $A,B$ subsets of $E$ , the following results hold: $\overline{\overline{A}}=\overline{A}$ , $A \subset B \Rightarrow \overline{A} \subset \overline{B}$ , $\overline{A \cup B} = \overline{A} \cup \overline{B}$ and $\overline{A \cap B} \subset \overline{A} \cap \overline{B}$ .

Let’s prove it.
$\overline{A}$ being closed, it is equal to its closure and $\overline{\overline{A}}=\overline{A}$ .

Suppose that $A \subset B$ . As $B \subset \overline{B}$ , we have $A \subset \overline{B}$ . Also, $\overline{B}$ is closed so it contains $\overline{A}$ , which proves $\overline{A} \subset \overline{B}$ .

Let’s consider $A,B \in E$ two subsets. As $A \subset A \cup B$ , we have $\overline{A} \subset \overline{A \cup B}$ and similarly $\overline{B} \subset \overline{A \cup B}$ . Hence $\overline{A} \cup \overline{B} \subset \overline{A \cup B}$ . Conversely, $A \cup B \subset \overline{A} \cup \overline{B}$ and $\overline{A} \cup \overline{B}$ is closed. So $\overline{A \cup B} \subset \overline{A} \cup \overline{B}$ and finally $\overline{A \cup B} = \overline{A} \cup \overline{B}$ .

Regarding the inclusion $\overline{A \cap B} \subset \overline{A} \cap \overline{B}$ , we notice that $A \cap B \subset \overline{A} \cap \overline{B}$ and that $\overline{A} \cap \overline{B}$ is closed to get the conclusion.

However, the implication $\overline{A} \subset \overline{B} \Rightarrow A \subset B$ doesn’t hold. For a counterexample, consider the space $E=\mathbb R$ equipped with the topology induced by the absolute value distance and take $A=[0,1)$ , $B=(0,1]$ . We have $\overline{A}=\overline{B}=[0,1]$ .

The equality $\overline{A} \cap \overline{B} = \overline{A \cap B}$ doesn’t hold as well. For the proof, just consider $A=[0,1)$ and $B=(1,2]$ . Continue reading Playing with interior and closure →

Analysis

A discontinuous real convex function

September 13, 2015 Jean-Pierre Merx Leave a comment

Consider a function $f$ defined on a real interval $I \subset \mathbb R$ . $f$ is called convex if: $\forall x, y \in I \ \forall \lambda \in [0,1]: \ f((1-\lambda)x+\lambda y) \le (1-\lambda) f(x) + \lambda f(y)$

Suppose that $I$ is a closed interval: $I=[a,b]$ with $a < b$ . For $a < s < t < u < b$ one can prove that: $\frac{f(t)-f(s)}{t-s}\le \frac{f(u)-f(s)}{u-s}\le\frac{f(u)-f(t)}{u-t}.$ It follows from those relations that $f$ has left-hand and right-hand derivatives at each point of the interior of $I$ . And therefore that $f$ is continuous at each point of the interior of $I$ .
Is a convex function defined on an interval $I$ continuous at all points of the interval? That might not be the case and a simple example is the function: $\begin{array}{l|rcl} f : & [0,1] & \longrightarrow & \mathbb R \\ & x & \longmapsto & 0 \text{ for } x \in (0,1) \\ & x & \longmapsto & 1 \text{ else}\end{array}$

It can be easily verified that $f$ is convex. However, $f$ is not continuous at $0$ and $1$ .

Math Counterexamples

Monthly Archives: September 2015

A group isomorphic to its automorphism group

Playing with interior and closure

Warm up with the closure operator

A discontinuous real convex function

Mathematical exceptions to the rules or intuition

Warm up with the closure operator

The case of an abelian group

Mathematical exceptions to the rules or intuition