Let $(X,d)$ be a metric space. Then a map $T : X \to X$ is called a contraction map if it exists $0 \le k < 1$ such that $$d(T(x),T(y)) \le k d(x,y)$$ for all $x,y \in X$. According to Banach fixed-point theorem, if $(X,d)$ is a complete metric space and $T$ a contraction map, then $T$ admits a fixed-point $x^* \in X$, i.e. $T(x^*)=x^*$.

We look here at counterexamples to the Banach fixed-point theorem when some hypothesis are not fulfilled.

First, let’s consider $$\begin{array}{l|rcl} f : & \mathbb R & \longrightarrow & \mathbb R \\ & x & \longmapsto & x+1 \end{array}$$ For all $x,y \in \mathbb R$ we have $\vert f(x)-f(y) \vert = \vert x- y \vert$. $f$ is not a contraction, but an isometry. Obviously, $f$ has no fixed-point.

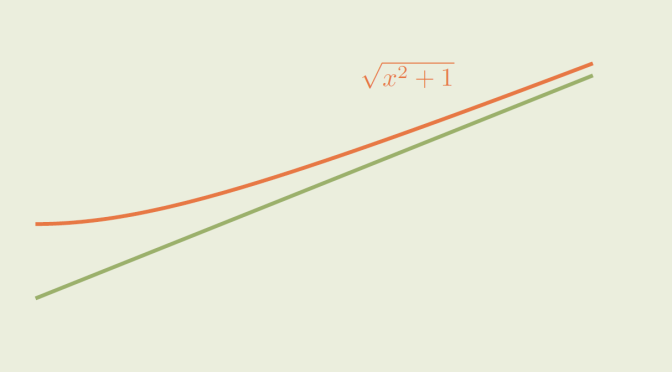
We now prove that a map satisfying $$d(g(x),g(y)) < d(x,y)$$ might also not have a fixed-point. A counterexample is the following map $$\begin{array}{l|rcl} g : & [0,+\infty) & \longrightarrow & [0,+\infty) \\ & x & \longmapsto & \sqrt{1+x^2} \end{array}$$ Since $$g^\prime(\xi) = \frac{\xi}{\sqrt{1+\xi^2}} < 1 \text{ for all } \xi \in [0, +\infty),$$ by the mean value theorem $$\vert g(x) - g(y)| = \vert g^\prime(\xi)\vert |x-y| < |x-y| \text{ for all } x, y \in [0, +\infty).$$ However $g$ has no fixed-point. Finally, let's have a look to a space $(X,d)$ which is not complete. We take $a,b \in \mathbb R$ with $0 < a < 1$ and for $(X,d)$ the space $X = \mathbb R \setminus \{\frac{b}{1-a}\}$ equipped with absolute value distance. $X$ is not complete. Consider the map $$\begin{array}{l|rcl} h : & X & \longrightarrow & X \\ & x & \longmapsto & ax + b \end{array}$$ $h$ is well defined as for $x \neq \frac{b}{1-a}$, $h(x) \neq \frac{b}{1-a}$. $h$ is a contraction map as for $x,y \in \mathbb R$ $$\vert h(x)-h(y) \vert = a \vert x - y \vert$$ However, $h$ doesn't have a fixed-point in $X$ as $\frac{b}{1-a}$ is the only real for which $h(x)=x$.