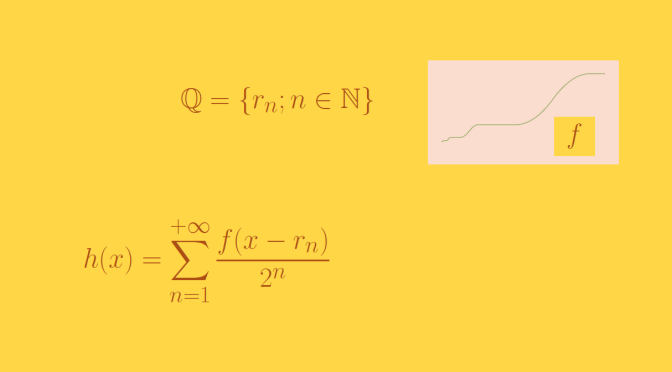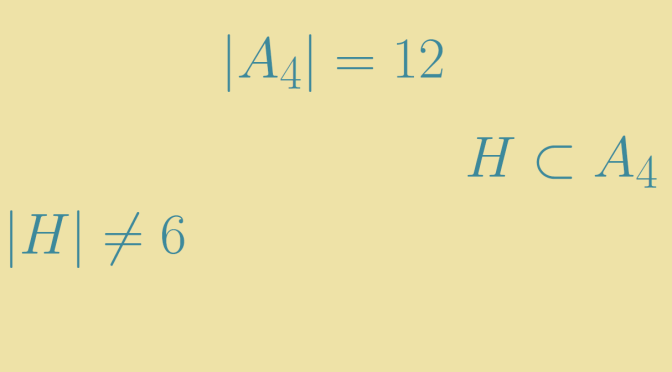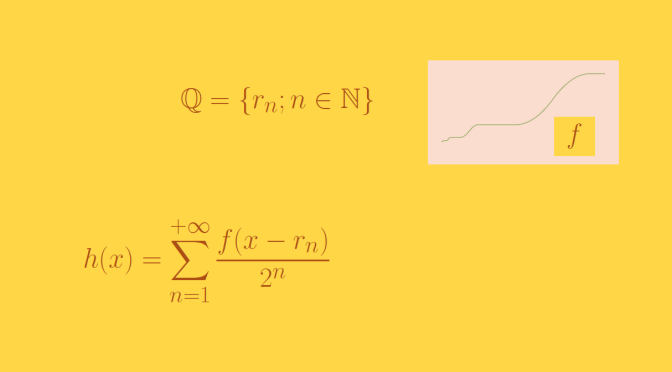
We build here a continuous function of one real variable whose derivative exists on \(\mathbb{R} \setminus \mathbb{Q}\) and doesn’t have a left or right derivative on each point of \(\mathbb{Q}\).
As \(\mathbb{Q}\) is (infinitely) countable, we can find a bijection \(n \mapsto r_n\) from \(\mathbb{N}\) to \(\mathbb{Q}\). We now reuse the function \(f\) defined here. Recall \(f\) main properties: Continue reading A continuous function not differentiable at the rationals but differentiable elsewhere →

We build here a continuous function of one real variable whose derivative exists except at \(0\) and is bounded on \(\mathbb{R^*}\).
We start with the even and piecewise linear function \(g\) defined on \([0,+\infty)\) with following values:
\[g(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x =0\\
0 & \mbox{if } x \in \{\frac{k}{4^n};(k,n) \in \{1,2,4\} \times \mathbb{N^*}\}\\
1 & \mbox{if } x \in \{\frac{3}{4^n};n \in \mathbb{N^*}\}\\
\end{array}
\right.
\]
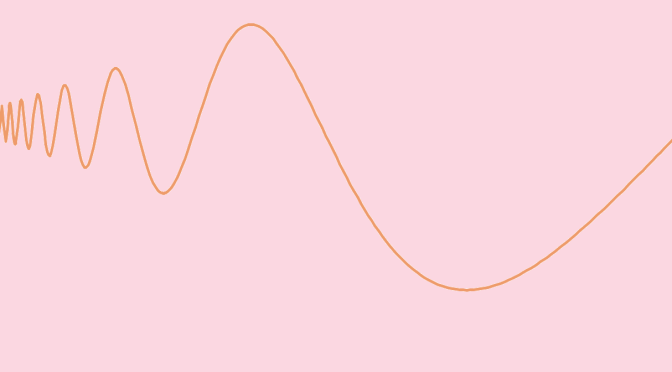
The picture below gives an idea of the graph of \(g\) for positive values. Continue reading A differentiable function except at one point with a bounded derivative →
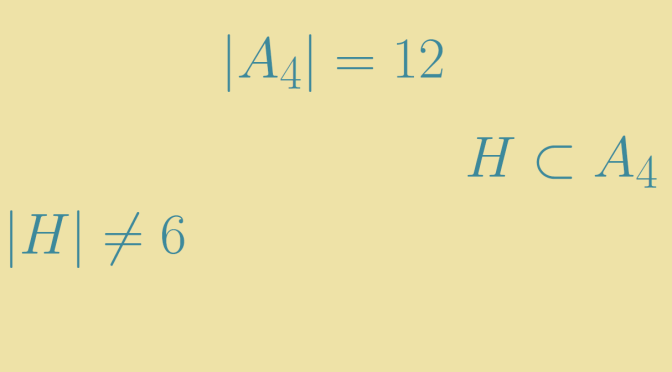
Lagrange’s theorem, states that for any finite group \(G\), the order (number of elements) of every subgroup \(H\) of \(G\) divides the order of \(G\) (denoted by \(\vert G \vert\)).
Lagrange’s theorem raises the converse question as to whether every divisor \(d\) of the order of a group is the order of some subgroup. According to Cauchy’s theorem this is true when \(d\) is a prime.
However, this does not hold in general: given a finite group \(G\) and a divisor \(d\) of \(\vert G \vert\), there does not necessarily exist a subgroup of \(G\) with order \(d\). The alternating group \(G = A_4\), which has \(12\) elements has no subgroup of order \(6\). We prove it below. Continue reading Converse of Lagrange’s theorem does not hold →
Introduction on total variation of functions
Recall that a function of bounded variation, also known as a BV-function, is a real-valued function whose total variation is bounded (finite).
Being more formal, the total variation of a real-valued function \(f\), defined on an interval \([a,b] \subset \mathbb{R}\) is the quantity:
\[V_a^b(f) = \sup\limits_{P \in \mathcal{P}} \sum_{i=0}^{n_P-1} \left\vert f(x_{i+1}) – f(x_i) \right\vert\] where the supremum is taken over the set \(\mathcal{P}\) of all partitions of the interval considered. Continue reading A continuous function which is not of bounded variation →

Introduction
We aim at defining a continuous function \(\varphi : [0,1] \rightarrow [0,1]^2\). At first sight this looks quite strange.
Indeed, \(\varphi\) cannot be a bijection. If \(\varphi\) would be bijective, it would also be an homeomorphism as a continuous bijective function from a compact space to a Haussdorff space is an homeomorphism. But an homeomorphism preserves connectedness and \([0,1] \setminus \{1/2\}\) is not connected while \([0,1]^2 \setminus \{\varphi(1/2)\}\) is.
Nor can \(\varphi\) be piecewise continuously differentiable as the Lebesgue measure of \(\varphi([0,1])\) would be equal to \(0\).
\(\varphi\) is defined in two steps using the Cantor space \(K\). Continue reading A curve filling a square – Lebesgue example →
Mathematical exceptions to the rules or intuition