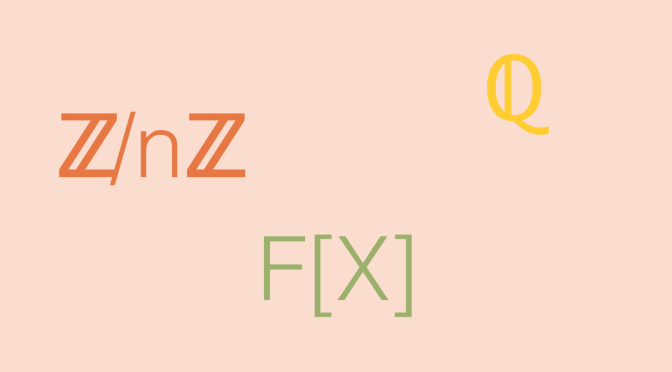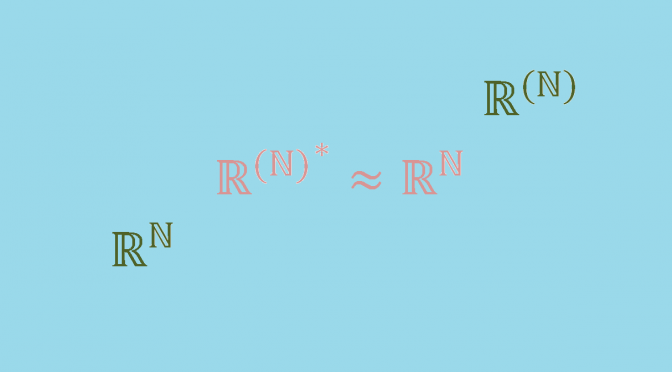
Definition of the Cantor set
The Cantor ternary set (named Cantor set below) \(K\) is a subset of the real segment \(I=[0,1]\). It is built by induction:
- Starting with \(K_0=I\)
- If \(K_n\) is a finite disjoint union of segments \(K_n=\cup_k \left[a_k,b_k\right]\), \[K_{n+1}=\bigcup_k \left(\left[a_k,a_k+\frac{b_k-a_k}{3}\right] \cup \left[a_k+2\frac{b_k-a_k}{3},b_k\right]\right)\]
And finally \(K=\displaystyle \bigcap_{n \in \mathbb{N}} K_n\). The Cantor set is created by repeatedly deleting the open middle third of a set of line segments starting with the segment \(I\).
The Cantor set is a closed set as it is an intersection of closed sets. Continue reading Cantor set: a null set having the cardinality of the continuum →
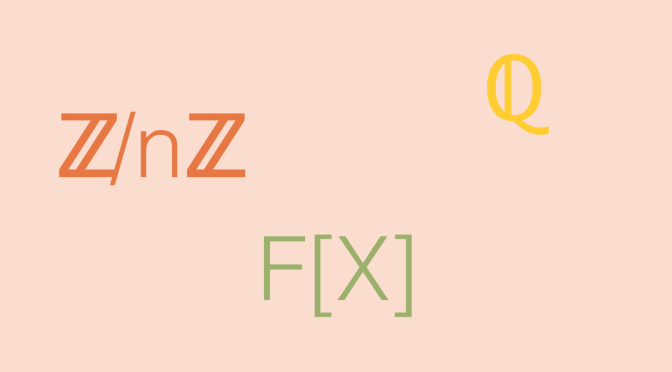
Let’s start by recalling some background about modules.
Suppose that \(R\) is a ring and \(1_R\) is its multiplicative identity. A left \(R\)-module \(M\) consists of an abelian group \((M, +)\) and an operation \(R \times M \rightarrow M\) such that for all \(r, s \in R\) and \(x, y \in M\), we have:
- \(r \cdot (x+y)= r \cdot x + r \cdot y\) (\( \cdot\) is left-distributive over \(+\))
- \((r +s) \cdot x= r \cdot x + s \cdot x\) (\( \cdot\) is right-distributive over \(+\))
- \((rs) \cdot x= r \cdot (s \cdot x)\)
- \(1_R \cdot x= x \)
\(+\) is the symbol for addition in both \(R\) and \(M\).
If \(K\) is a field, \(M\) is \(K\)-vector space. It is well known that a vector space \(V\) is having a basis, i.e. a subset of linearly independent vectors that spans \(V\).
Unlike for a vector space, a module doesn’t always have a basis. Continue reading A module without a basis →
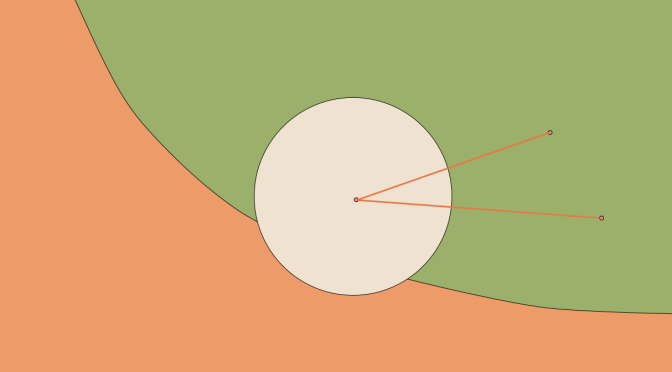
We consider a normed vector space \(E\) over the field of the reals \(\mathbb{R}\) and a convex subset \(C \subset E\).
We suppose that \(0 \in C\) and that \(C\) is unbounded, i.e. there exists points in \(C\) at distance as big as we wish from \(0\).
The following question arises: “does \(C\) contains a ray?”. It turns out that the answer depends on the dimension of the space \(E\). If \(E\) is of finite dimension, then \(C\) always contains a ray, while if \(E\) is of infinite dimension \(C\) may not contain a ray. Continue reading An unbounded convex not containing a ray →
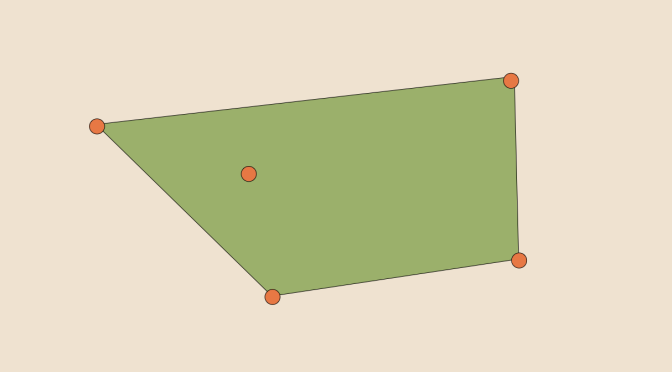
We consider a topological vector space \(E\) over the field of the reals \(\mathbb{R}\). The convex hull of a subset \(X \subset E\) is the smallest convex set that contains \(X\).
The convex hull may also be defined as the intersection of all convex sets containing X or as the set of all convex combinations of points in X.
The convex hull of \(X\) is written as \(\mbox{Conv}(X)\). Continue reading A compact whose convex hull is not compact →
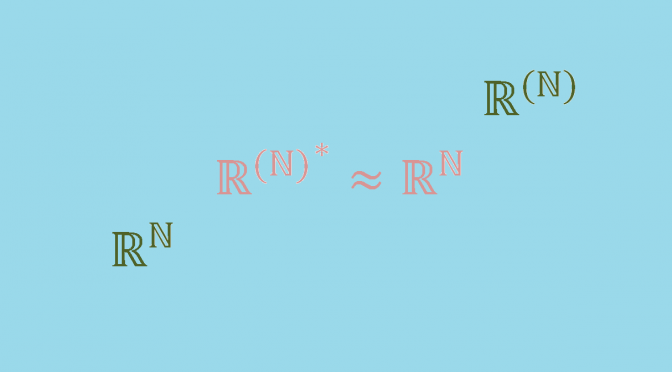
In this page \(\mathbb{F}\) refers to a field. Given any vector space \(V\) over \(\mathbb{F}\), the dual space \(V^*\) is defined as the set of all linear functionals \(f: V \mapsto \mathbb{F}\). The dual space \(V^*\) itself becomes a vector space over \(\mathbb{F}\) when equipped with the following addition and scalar multiplication:
\[\left\{
\begin{array}{lll}(\varphi + \psi)(x) & = & \varphi(x) + \psi(x) \\
(a \varphi)(x) & = & a (\varphi(x)) \end{array} \right. \] for all \(\phi, \psi \in V^*\), \(x \in V\), and \(a \in \mathbb{F}\).
There is a natural homomorphism \(\Phi\) from \(V\) into the double dual \(V^{**}\), defined by \((\Phi(v))(\phi) = \phi(v)\) for all \(v \in V\), \(\phi \in V^*\). This map \(\Phi\) is always injective. Continue reading A vector space not isomorphic to its double dual →
Mathematical exceptions to the rules or intuition